Cho hình thàng ABCD (AB//CD), O là giao điểm của 2 đường chéo. Gọi A' và B' theo thứ tự là điểm đối xứng của A và B qua đường phân giác góc AOB. Chứng minh rằng: \(\widehat{ACA'}=\widehat{BDB'}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét tứ giác BOCM có
I là trung điểm chung của BC và OM
=>BOCM là hbh
=>OC//BM và OC=BM
Xét tứ giác DOCN có
K là trung điểm chung của DC và ON
=>DOCN là hbh
=>DN//OC và DN=OC
=>DN//BM và DN=BM
=>BDNM là hbh
c: BO//CM
NC//DO
mà B,O,D thẳng hàng
nên M,C,N thẳng hàng

Hình:

Giải:
a) Ta có:
\(\left\{{}\begin{matrix}BH=HC\\MH=HO\end{matrix}\right.\)
Nên tứ giác BMCO là hình bình hành
\(\Rightarrow\left\{{}\begin{matrix}BM//OC\\BM=OC\end{matrix}\right.\left(1\right)\)
Tương tự, tứ giác OCND là hình bình hành
\(\Rightarrow\left\{{}\begin{matrix}DN//OC\\DN=OC\end{matrix}\right.\left(2\right)\)
Từ (1) và (2)
\(\Rightarrow\left\{{}\begin{matrix}BM//DN\\BM=OC=DN\end{matrix}\right.\)
Suy ra tứ giác BMND là hình bình hành
b) Để hình bình hành BMND trở thành hình chũ nhật thì BM⊥BD
Đồng thời BM//AC
Nên AC⊥BD
c) Vì BMCO là hình bình hành nên MC//BD (3)
Và BMND là hình bình hành nên MN//BD (4)
Từ (3) và (4), suy ra M,N,C thẳng hàng (theo tiên đề Ơ-clit)
Vậy ...

O là giao điểm của hai đường chéo AC,BD(gt)
=> AO=OC, OD=OB (vì ABCD là hình bình hành)
Lại có;
E là trung điểm của OD(gt)
=> OE=1/2.OD
F là trung điểm của OB(gt)
=> OF=1/2.OB
Mà OD=OB (cmt)
=> OE=OF
Tứ giác AFCE có: OA=OC(cmt) và OE=OF(cmt)
=> O là giao điểm của hai đường chéo AC,EF cắt nhau tại trung điểm mỗi đoạn
=> AFCE là hình bình hành
=> AE//CF (vì AE, CF là hai cạnh đối nhau)
Có AE//CF (cmt) => EK// CF (vì K thuộc AE)
Từ O vẽ đường thẳng cắt CD tại H sao cho OH//EK//CF
Xét tam giác DOH có: E là trung điểm của OD
EK//OH (theo cách vẽ đường thẳng OH)
=> K là trung điểm của DH
=> DK=KH (1)
Xét hình thang EKCF có: O là trung điểm của EF (theo câu a)
OH//EK//CF (theo cách vẽ đường thẳng OH)
=> H là trung điểm của KC
=> KH=HC (2)
Từ (1) và (2) => DK=KH=HC
Lại có: KC=KH+HC => KC= DK+DK (vì DK=KH=HC)
=> KC=2DK => DK=1/2KC

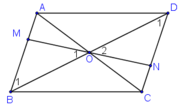
+ ABCD là hình bình hành có O là giao điểm hai đường chéo
⇒ OB = OD.
+ ABCD là hình bình hành ⇒ AB // CD ⇒ 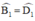 (Hai góc SLT).
(Hai góc SLT).
Hai tam giác BOM và DON có:
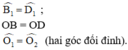
⇒ ΔBOM = ΔDON (g.c.g)
⇒ OM = ON
⇒ O là trung điểm của MN
⇒ M đối xứng với N qua O.

Xét tứ giác OBMC ta có
2 đường chéo BC và OM cắt nhau tại I
I là trung điểm BC (gt)
I là trung điểm OM ( M là điểm đối xứng của O qua I)
-> tứ giác OBMC là hbh
cmtt tứ giác ODNC là hbh
ta có
BM // OC ( OBMC là hbh)
DN // OC (ODNC là hbh)
-.> BM//CN
ta có
BM // OC ( OBMC là hbh)
DN // OC (ODNC là hbh)
-.> BM//CN // OC
ta có
BM = OC ( OBMC là hbh)
DN = OC (ODNC là hbh)
-.> BM = ON
Xét tứ giác BMND ta có
BM // ON (cmt)
BM = ON (cmt)
-> tứ giác BMND là hbh
b) giả sử BMND là hcn
ta có
MB vuông góc BD ( BNMD là hcn)
BM // OC ( OBMC là hbh)
-> BD vuông góc OC tại O
Vậy AC vuông góc BD thì BMND là hcn
c) ta có
BD // CM ( OB // CM ; O thuộc BD)
BD // CN ( OD //CN . O thuộc BD)
-> CM trùng CN
-> C,N,M thẳng hàng

Bài giải:
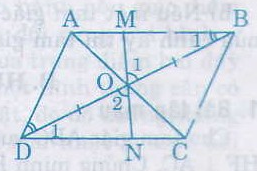
Hai tam giác BOM và DON có
ˆB1B1^ = ˆD1D1^ (so le trong)
BO = DO (tính chất)
ˆO1O1^ = ˆO2O2^ (đối đỉnh)
nên ∆BOM = ∆DON (g.c.g)
Suy ra OM = ON.
O là trung điểm của MN nên M đối xứng với N qua O
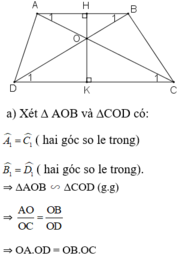
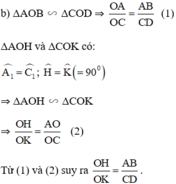
Gọi Od là phân giác của \(\widehat{AOB}\)
Vì \(\widehat{\text{B'}}\) đối xứng với \(\widehat{B}\) qua Od\(\Rightarrow OB'=OB.\widehat{B'Od}=\widehat{dOB}\)
\(\Rightarrow\widehat{B'Od}=\widehat{AOd}\)(vì Od là phân giác của góc O)
\(\Rightarrow O,B',A\)thẳng hàng.
Tương tự\(\rightarrow O,B',A\)thẳng hàng\(\rightarrow OA=OA'\)
Vì AA'\(\perp\)Od,BB'\(\perp\)Od,\(\rightarrow AA'//BB'\)vì A,A' đối xứng qua Od;B,B' đối xứng qua Od
Ta có:\(AB//CD\rightarrow\frac{OA}{OC}=\frac{OB}{OD}\)
\(\rightarrow\frac{OA}{OC+OA}=\frac{OB}{OD+OB}\)
\(\rightarrow\frac{CA}{DB}=\frac{OA}{OB}=\frac{OA}{OB'}\)
\(\rightarrow\frac{CA}{DB}=\frac{AA'}{BB'}\)vì\(AA'//BB'\left(\perp Od\right)\)
Mà\(\widehat{OAA'}=90^o-\frac{1}{2}\widehat{AOA'}=90^o-\frac{1}{2}\widehat{B'OB}\)
\(=\widehat{B'OB}\left(OA=OA',OB=OB'\right)\)
\(\Delta CAA'~\Delta BDB'\left(g.g\right)\)
\(\Rightarrow\widehat{ACA'}=\widehat{BDB'}\)