Tìm x thuộc \(ℕ\) biết:
\(\dfrac{1}{1.3}+\dfrac{1}{3.5}+\dfrac{1}{5.7}+...+\dfrac{1}{\left(2x+1\right)}+\dfrac{1}{\left(2x+3\right)}=\dfrac{2022}{2023}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\Leftrightarrow\dfrac{1}{2}\left[\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+...+\dfrac{2}{\left(2x-1\right)\left(2x+1\right)}\right]=\dfrac{49}{99}\\ \Leftrightarrow1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{2x-1}-\dfrac{1}{2x+1}=\dfrac{98}{99}\\ \Leftrightarrow1-\dfrac{1}{2x+1}=\dfrac{98}{99}\\ \Leftrightarrow\dfrac{1}{2x+1}=\dfrac{1}{99}\\ \Leftrightarrow2x+1=99\Leftrightarrow x=49\)

\(\Leftrightarrow\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+...+\dfrac{2}{\left(2x-1\right)\left(2x+1\right)}=\dfrac{98}{99}\\ \Leftrightarrow1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{2x-1}-\dfrac{1}{2x+1}=\dfrac{98}{99}\\ \Leftrightarrow1-\dfrac{1}{2x+1}=\dfrac{98}{99}\\ \Leftrightarrow\dfrac{2x+1-1}{2x+1}=\dfrac{98}{99}\Leftrightarrow198x=196x+98\\ \Leftrightarrow2x=98\Leftrightarrow x=49\)

a, \(\dfrac{1}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{2x-1}-\dfrac{1}{2x+1}\right)=\dfrac{49}{99}\)
\(\Leftrightarrow\dfrac{1}{2}.\left(1-\dfrac{1}{2x+1}\right)=\dfrac{49}{99}\)
\(\Leftrightarrow\dfrac{2x+1-1}{2x+1}=\dfrac{98}{99}\)
\(\Leftrightarrow98\left(2x+1\right)=99.2x\)
\(\Leftrightarrow2x=98\Rightarrow x=49\)
b: Đặt \(A=1-3+3^2-3^3+...+\left(-3\right)^x\)
\(=\left(-3\right)^0+\left(-3\right)^1+\left(-3\right)^2+...+\left(-3\right)^x\)
\(\Leftrightarrow-3A=\left(-3\right)^1+\left(-3\right)^2+...+\left(-3\right)^{x+1}\)
\(\Leftrightarrow-3A-A=\left(-3\right)^1+\left(-3\right)^2+...+\left(-3\right)^{x+1}-...-1\)
\(\Leftrightarrow-4A=\left(-3\right)^{x+1}-1\)
\(\Leftrightarrow A=\dfrac{\left(-3\right)^{x+1}-1}{-4}=\dfrac{-\left(-3\right)^{x+1}+1}{4}\)
\(\Leftrightarrow\dfrac{-\left(-3\right)^{x+1}+1}{4}=\dfrac{3^{2012}-1}{2}\)
\(\Leftrightarrow-\left(-3\right)^{x+1}+1=2\cdot3^{2012}-2\)
\(\Leftrightarrow-\left(-3\right)^{x+1}=2\cdot3^{2012}-3\)
\(\Leftrightarrow-\left(-3\right)^{x+1}=3\left(2\cdot3^{2011}-1\right)\)
\(\Leftrightarrow-\left(-3\right)^x=2\cdot3^{2011}-1\)
=>x=2010

Ta có: \(\dfrac{1}{1\cdot3}+\dfrac{1}{3\cdot5}+\dfrac{1}{5\cdot7}+...+\dfrac{1}{x\left(x+2\right)}=\dfrac{20}{41}\)
\(\Leftrightarrow\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+...+\dfrac{2}{x\left(x+2\right)}=\dfrac{40}{41}\)
\(\Leftrightarrow1-\dfrac{2}{x+2}=\dfrac{40}{41}\)
\(\Leftrightarrow\dfrac{2}{x+2}=\dfrac{1}{41}\)
Suy ra: x+2=82
hay x=80

Dat A=\(\dfrac{1}{1.3}+\dfrac{1}{3.5}+...+\dfrac{1}{13.15}\)
2A=\(\dfrac{2}{1.3}+\dfrac{2}{3.5}+...+\dfrac{2}{13.15}\)
= 1-\(\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-....+\dfrac{1}{13}-\dfrac{1}{15}\)
= 1-\(\dfrac{1}{15}=\dfrac{14}{15}\)
=> A=\(\dfrac{7}{15}\)
Ta co : \(\dfrac{7}{15}\left(x-1\right)=\dfrac{3}{5}x-\dfrac{7}{15}\)
=> \(\dfrac{7}{15}x-\dfrac{7}{15}+\dfrac{7}{15}=\dfrac{3}{5}x\)
=> \(\dfrac{7}{15}x-\dfrac{3}{5}x=0\)
=> x\(\left(\dfrac{7}{15}-\dfrac{3}{5}\right)=0\)
=> x\(\left(-\dfrac{2}{15}\right)=0\)
=> x=0
\(\left(\dfrac{1}{1.3}+\dfrac{1}{3.5}+\dfrac{1}{5.7}+...+\dfrac{1}{13.15}\right)\left(x-1\right)=\dfrac{3}{5}x-\dfrac{7}{15}\)
<=>\(\dfrac{1}{2}\left(\dfrac{2}{1.3}+\dfrac{2}{3.5}+\dfrac{2}{5.7}+...+\dfrac{2}{13.15}\right)\left(x-1\right)=\dfrac{3}{5}x-\dfrac{7}{15}\)
<=>\(\dfrac{1}{2}\left(\dfrac{1}{1}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{13}-\dfrac{1}{15}\right)\left(x-1\right)=\dfrac{3}{5}x-\dfrac{7}{15}\)
<=>\(\dfrac{1}{2}\left(\dfrac{1}{1}-\dfrac{1}{15}\right)\left(x-1\right)=\dfrac{3}{5}x-\dfrac{7}{15}\)
<=> \(\dfrac{7}{15}\left(x-1\right)=\dfrac{3}{5}x-\dfrac{7}{15}\)
<=>\(\dfrac{7}{15}x-\dfrac{7}{15}=\dfrac{3}{5}x-\dfrac{7}{15}\)
<=>\(\dfrac{7}{15}x-\dfrac{3}{5}x=\dfrac{-7}{15}+\dfrac{7}{15}\)
<=> \(\dfrac{-2}{15}x=0\)
<=> \(x=0\)
Vậy: \(s=\left\{0\right\}.\)

b) Vì \(\left|x+\dfrac{1}{1.3}\right| \ge0;\left|x+\dfrac{1}{3.5}\right|\ge0;...;\left|x+\dfrac{1}{97.99}\right|\ge0\)
\(\Rightarrow50x\ge0\Rightarrow x\ge0\)
Khi đó: \(\left|x+\dfrac{1}{1.3}\right|=x+\dfrac{1}{1.3};\left|x+\dfrac{1}{3.5}\right|=x+\dfrac{1}{3.5};...;\left|x+\dfrac{1}{97.99}\right|=x+\dfrac{1}{97.99}\left(1\right)\)
Thay (1) vào đề bài:
\(x+\dfrac{1}{1.3}+x+\dfrac{1}{3.5}+...+x+\dfrac{1}{97.99}=50x\)
\(\Rightarrow\left(x+x+...+x\right)+\left(\dfrac{1}{3.5}+\dfrac{1}{5.7}+...+\dfrac{1}{97.99}\right)=50x\)
\(\Rightarrow49x+\left[\dfrac{1}{2}\left(\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{97}-\dfrac{1}{99}\right)\right]=50x\)
\(\Rightarrow49x+\dfrac{16}{99}=50x\)
\(\Rightarrow x=\dfrac{16}{99}\)
Vậy \(x=\dfrac{16}{99}.\)

\(\dfrac{1}{1\cdot3}+\dfrac{1}{3\cdot5}+...+\dfrac{1}{\left(2x-1\right)\left(2x+1\right)}=\dfrac{49}{99}\\ \Leftrightarrow2\left(\dfrac{1}{1\cdot3}+\dfrac{1}{3\cdot5}+...+\dfrac{1}{\left(2x-1\right)\left(2x+1\right)}\right)=2\cdot\dfrac{49}{99}\\ \Leftrightarrow\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+...+\dfrac{2}{\left(2x-1\right)\left(2x+1\right)}=\dfrac{98}{99}\\ \Leftrightarrow\dfrac{1}{1}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{2x-1}-\dfrac{1}{2x+1}=\dfrac{98}{99}\\ \Leftrightarrow1-\dfrac{1}{2x+1}=1-\dfrac{1}{99}\\ \Leftrightarrow\dfrac{1}{2x+1}=\dfrac{1}{99}\\ \Rightarrow2x+1=99\\ \Leftrightarrow2x=98\\ \Leftrightarrow x=49\)
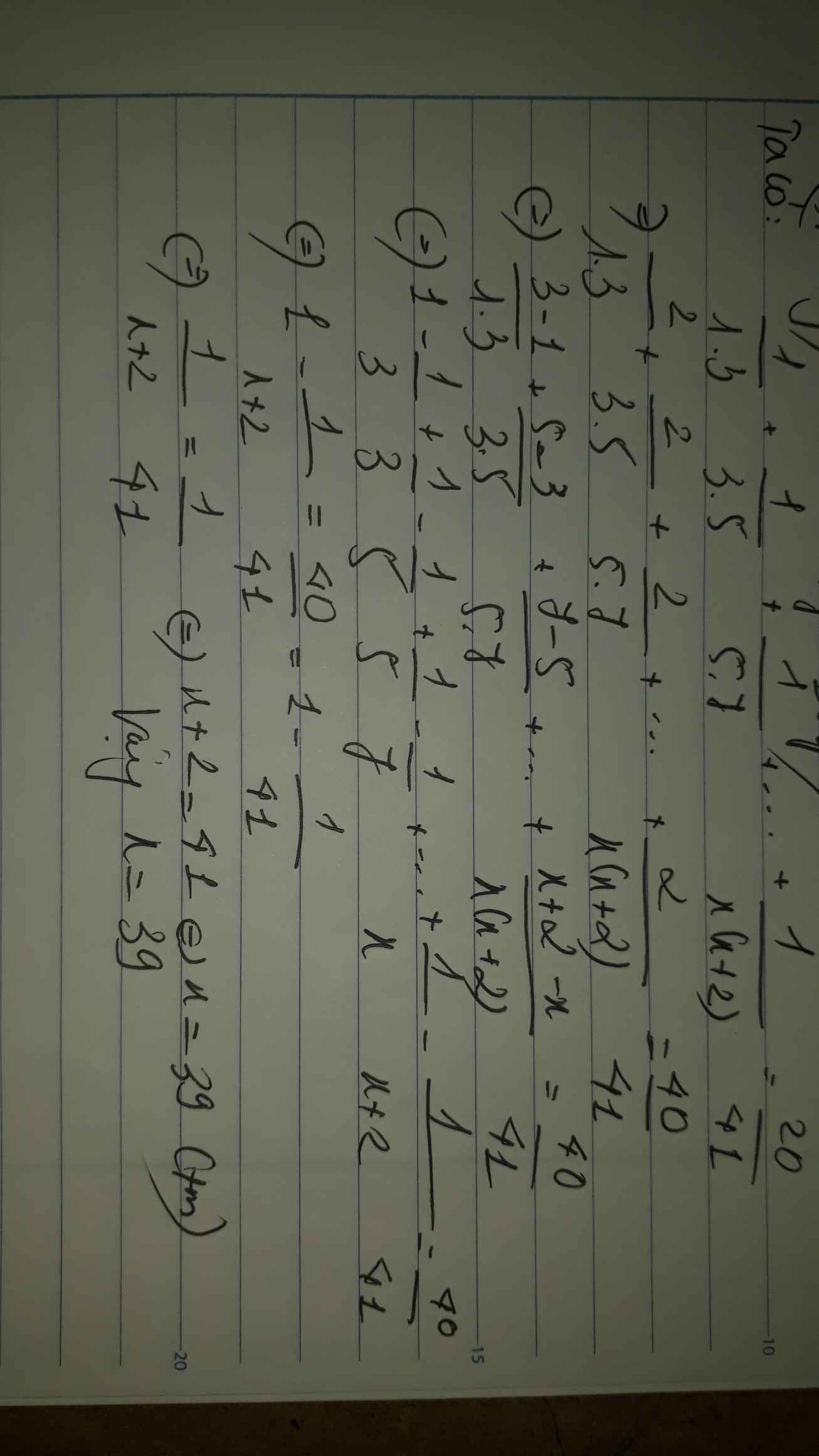
Đề bài chuẩn chưa em nhỉ?
dạ đề đúng ạ, e lấy ở đề thi toán trường em ấy ạ