Cho a=2.3.4.5.6 ... 2014.2015.2016 Các số trong dãy a+2; a+3; a+4; ... ;a+2015; a+2016 là số nguyên tố hay hợp số
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) chia hết cho 2, chia hết cho 5
b) chia hết cho 2, ko chia hết cho 5
c) chia hết cho 2, ko chia hết cho 5
d) ko chia hết cho 2, chia hết cho 5
e) ko chia hết cho 2, chia hết cho 5
f) ko chia hết cho 2, chia hết cho 5
a: Biểu thức này chia hết cho cả 2 và 5
b: Biểu thức này chia hết cho 2 nhưng không chia hết cho 5
c: Biểu thức này chia hết cho 2 nhưng ko chia hết cho 5
d: Biểu thức này chia hết cho 5 nhưng không chia hết cho 2
e: Biểu thức này chia hết cho 5 nhưng không chia hết cho 2
f: Biểu thức này chia hết cho 5 nhưng không chia hết cho 2


a) \(\left\{{}\begin{matrix}2.3.4.5.6⋮2\\82⋮2\end{matrix}\right.\)\(\Rightarrow2.3.4.5.6+82⋮2\)
\(\left\{{}\begin{matrix}2.3.4.5.6⋮5\\82⋮̸5\end{matrix}\right.\)\(\Rightarrow2.3.4.5.6+82⋮̸5\)
b) \(\left\{{}\begin{matrix}2.3.4.5.6⋮2\\95⋮̸2\end{matrix}\right.\)\(\Rightarrow2.3.4.5.6-95⋮̸2\)
\(\left\{{}\begin{matrix}2.3.4.5.6⋮5\\95⋮5\end{matrix}\right.\)\(\Rightarrow2.3.4.5.6-95⋮5\)

A=2011.2012.2013+2014.2015.2016
= (....6)+(....0)= (...6)
Vậy cs tận cùng là 6

lấy chữ số của các thừ số nhân với nhau:
1.2.3=6 => 2011.2012.2013 có chữ số tận cùng là 6.
4.5.6=120 => 2014.2015.2016 có chữ số tận cùng là 0.
Vậy 2011.2012.2013+2014.2015.2016=(...6)+(....0)=....6
Có chữ số tận cùng là 6.
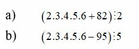
Ta có: - \(a⋮2\)(vì trong tích có thừa số 2) và \(2⋮2\)=> \(a+2⋮2\)=> a + 2 là hợp số.
- \(a⋮3\)(vì trong tích có thừa số 3) và \(3⋮3\)=> \(a+3⋮3\)=> a + 3 là hợp số.
...
- \(a⋮2016\)(vì trong tích có thừa số 2016) và \(2016⋮2016\)=> \(a+2016⋮2016\)=> a + 2016 là hợp số.
Vậy các số trong dãy a+2; a+3; a+4; ... ; a+2015; a+2016 đều là hợp số.