1) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình:
Một mảnh đất hình chữ nhật có chiều dài lớn hơn chiều rộng $3 $m. Nếu tăng chiều dài thêm $2$m và giảm chiều rộng $1 $m thì diện tích mảnh đất không đổi. Tính chiều dài và chiều rộng ban đầu của mảnh đất.
2) Một hình trụ có đường kính đáy là $1,2 $m và chiều cao là $1,8 $m. Tính thể tích hình trụ đó (kết quả làm tròn đến số thập phân thứ nhất, lấy $\pi \approx 3,14$ ).

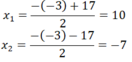
Bài giải
1,gọi chiều rộng mảnh vườn là x(m)
chiều dài mảnh vườn là x+3 (m) (x>0)
vì tăng chiều dài thêm 2m và giảm chiều rộng 1m thì diện tích mảnh vườn không đổi nên ta có pt:
(x-1)(x+5)=x(x+3)
⇔\(x^2+5x-x-5=x^2+3x\Leftrightarrow x^2-x^2+5x-x-3x=5\Leftrightarrow x=5\) (TM)
vậy chiều rộng mảnh vườn là 5m
chiều dài mảnh vườn là 5+3=8m
2,bán kính đáy của hình trụ là 1,2:2= 0,6 (m)
thể tích của hình trụ là : V = 3,14.(0,6)\(^2\).1,8=2 (m\(^3\))
vậy thể tích của hình trụ đó là 2m\(^3\)