Cứu e ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔADI và ΔAEI có
AD=AE
\(\widehat{DAI}=\widehat{EAI}\)
AI chung
DO đó: ΔADI=ΔAEI
Suy ra: DI=EI
hay I là trung điểm của DE
b: Xét ΔNID vuông tại I và ΔNIE vuông tại I có
NI chung
ID=IE
Do đó: ΔNID=ΔNIE
Suy ra: ND=NE

\(\left(1\right)FeCl_2+2NaOH\to Fe\left(OH\right)_2\downarrow +2NaCl\\ \left(2\right)Fe\left(OH\right)_2\xrightarrow{t^0}FeO+H_2O\\ \left(3\right)FeO+C\to Fe+CO\uparrow \\ \left(4\right)2Fe+3Cl_2\xrightarrow[]{t^o}2FeCl_3\\ \left(5\right)FeCl_3+3NaOH\to Fe\left(OH\right)_3\downarrow +3NaCl\\ \left(6\right)2Fe\left(OH\right)_3\xrightarrow{t^o}Fe_2O_3+3H_2O\\ \left(7\right)Fe_2O_3+3CO\xrightarrow{t^o}2Fe+3CO_2\\ \left(8\right)Fe+2HCl\to FeCl_2+H_2\)

Bài 1
a) \(2^{11}.64=2^{11}.2^6=2^{17}\)
Do \(16< 17\Rightarrow2^{16}< 2^{17}\)
Vậy \(2^{16}< 2^{11}.64\)
b) Do \(18>17\Rightarrow9^{18}>9^{17}\) (1)
\(9^{18}=\left(3^2\right)^{18}=3^{36}\)
Do \(36< 37\Rightarrow3^{36}< 3^{37}\)
\(\Rightarrow9^{18}< 3^{37}\) (2)
Từ (1) và (2) \(\Rightarrow9^{17}< 3^{37}\)
c) \(2^{333}=\left(2^3\right)^{111}=8^{111}\)
\(3^{222}=\left(3^2\right)^{111}=9^{111}\)
Do \(8< 9\Rightarrow8^{111}< 9^{111}\)
Vậy \(2^{333}< 3^{222}\)
d) \(3^{50}=\left(3^2\right)^{25}=9^{25}\)
Do \(9< 11\Rightarrow9^{25}< 11^{25}\)
Vậy \(3^{50}< 11^{25}\)
e) \(37< 38\Rightarrow3^{37}< 3^{38}\) (1)
Lại có: \(3^{38}=3^{2.19}=\left(3^2\right)^{19}=9^{19}\)
Do \(9< 10\Rightarrow9^{19}< 10^{19}\)
\(\Rightarrow3^{38}< 10^{19}\) (2)
Từ (1) và (2) \(\Rightarrow3^{37}< 10^{19}\)
f) Do \(17>16\Rightarrow17^{14}>16^{14}\) (1)
Do \(32>31\Rightarrow32^{11}>31^{11}\) (2)
Lại có:
\(16^{14}=\left(2^4\right)^{14}=2^{56}\)
\(32^{11}=\left(2^5\right)^{11}=2^{55}\)
Do \(56>55\Rightarrow2^{56}>2^{55}\)
\(\Rightarrow16^{14}>32^{11}\) (3)
Từ (1), (2) và (3) \(\Rightarrow17^{14}>31^{11}\)
Bài 2:
a) \(2^n-64=0\)
\(2^n=64\)
\(2^n=2^6\)
\(n=6\)
b) \(5.3^{n-3}-405=0\)
\(5.3^{n-3}=405\)
\(3^{n-3}=405:5\)
\(3^{n-3}=81\)
\(n-3=4\)
\(n=4+3\)
\(n=7\)
c) \(4^n.8=2^{15}\)
\(\left(2^2\right)^n.2^3=2^{15}\)
\(2^{2n}.2^3=2^{15}\)
\(2^{2n+3}=2^{15}\)
\(2n+3=15\)
\(2n=15-3\)
\(2n=12\)
\(n=12:2\)
\(n=6\)
d) \(3.2^{n+1}+2^{n+2}=160\)
\(2^{n+1}.\left(3+2\right)=160\)
\(2^{n+1}.5=160\)
\(2^{n+1}=160:5\)
\(2^{n+1}=32\)
\(2^{n+1}=2^5\)
\(n+1=5\)
\(n=5-1\)
\(n=4\)


3:
a: Xét ΔACH vuông tại H và ΔBCA vuông tại A có
góc C chung
=>ΔACH đồng dạng vơi ΔBCA
b: Xét ΔABC vuông tại A có AH là đường cao
nên AH^2=HB*HC

(x + 3)/3 = x/(-12)
-12.(x + 3) = 3x
-12x - 36 = 3x
-12x - 3x = 36
-15x = 36
x = -36/15
x = -12/5

1 wears - is wearing
2 are watching - watch
3 have - am having
4 are cleaning - clean
5 reads - is reading
1 wears,is wearing
2,are watching, watch
3,have, am having
4,are cleaning, clean
5,reads, is reading

Bài 60:
a: Xét ΔMNP có
B là trung điểm của NP
A là trung điểm của MN
Do đó: AB là đường trung bình của ΔMNP
Suy ra: AB//MP và \(AB=\dfrac{MP}{2}\)
hay MP=10cm
b: Xét tứ giác ABPM có AB//PM
nên ABPM là hình thang
mà \(\widehat{PMA}=90^0\)
nên ABPM là hình thang vuông
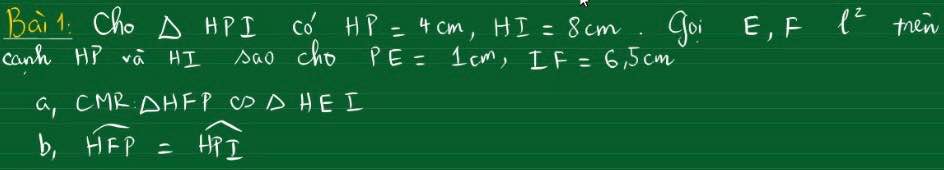


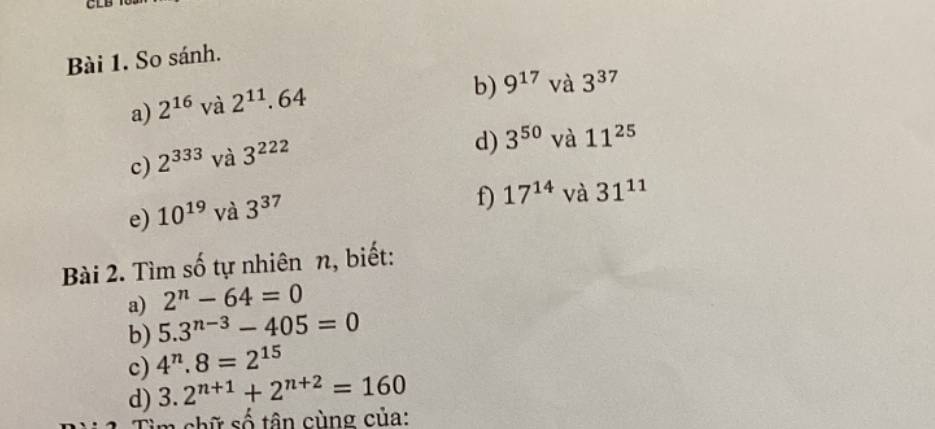
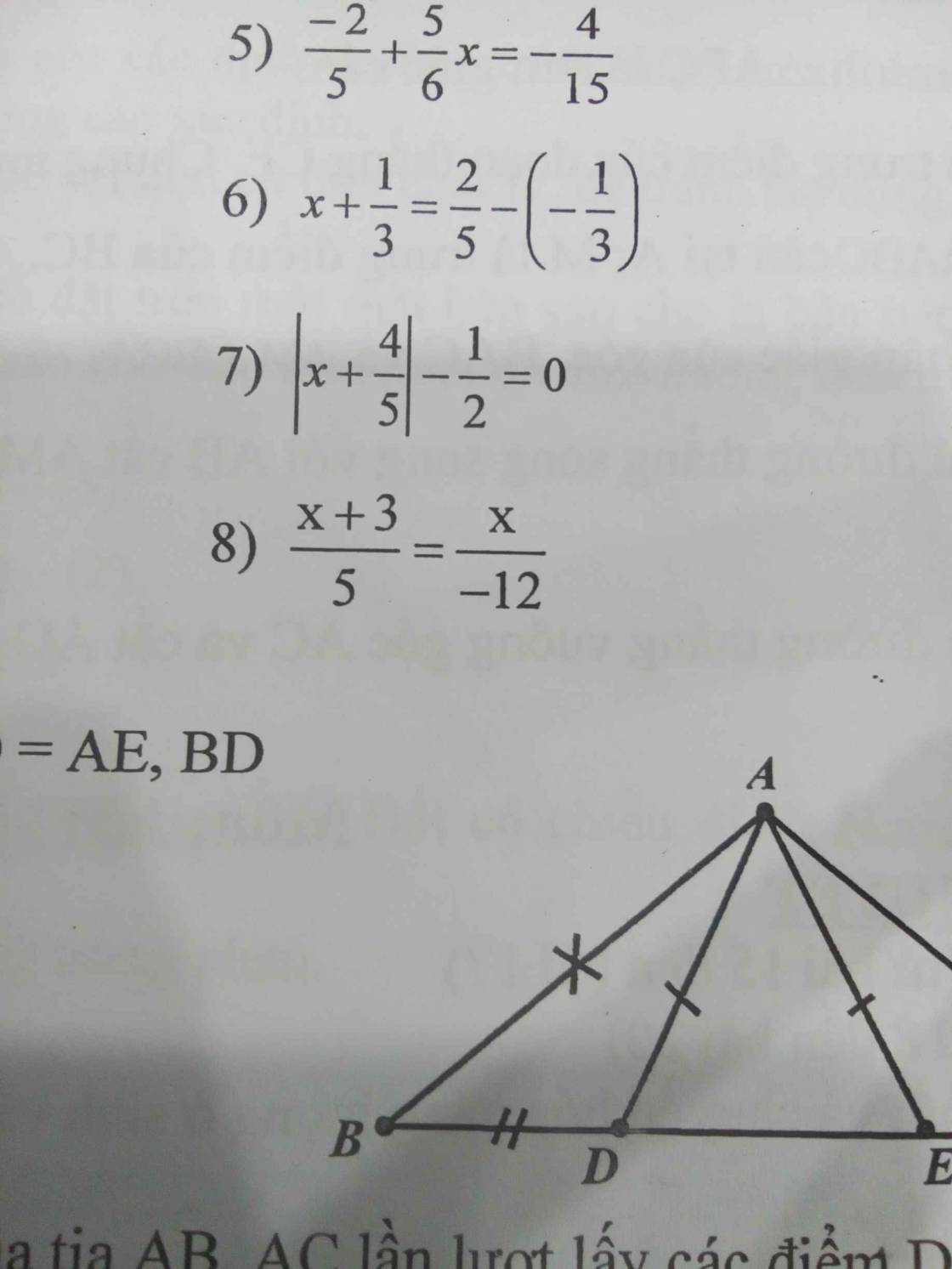
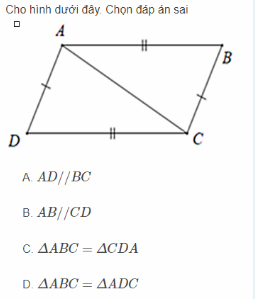 gấp gấp cứu e ạ
gấp gấp cứu e ạ





Bán kính hình tròn là:
\(12,56:3,14:2=2\left(cm\right)\)
Độ dài cạnh hình vuông là:
\(2\times2=4\left(cm\right)\)
Diện tích hình vuông là:
\(4\times4=16\left(cm^2\right)\)
Diện tích hình tròn là:
\(2\times2\times3,14=12,56\left(cm^2\right)\)
Diện tích phần tô đậm là:
\(16-12,56=3,44\left(cm^2\right)\)