Cho đường tròn tâm O bán kính R, kẻ đường kính AB. Gọi d là tiếp tuyến của (O) tại A. Lấy C là một điểm bất kì trên d (điểm C khác điểm A). Từ C kẻ tiếp tuyến thứ hai CM với (O) (M là tiếp điểm). Kẻ MH vuông góc với AB tại H. Gọi E là giao điểm của CO và MA, gọi K là giao điểm của CB và MH.
1) Chứng minh tứ giác AOMC nội tiếp.
2) Chứng minh EA.MH = EO.HA.
3) Kéo dài BM cắt d tại N. Chứng minh C là trung điểm của AN và KE // AB.
4) Qua O vẽ đường thẳng vuông góc với OC, đường thẳng này cắt các tia CA và CM theo thứ tự tại P và Q. Xác định vị trí của C để diện tích tam giác CPQ nhỏ nhất.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1: Xét tứ giác AMBO có
\(\widehat{OAM}+\widehat{OBM}=90^0+90^0=180^0\)
=>AMBO là tứ giác nội tiếp đường tròn đường kính OM
2: ΔONP cân tại O
mà OK là trung tuyến
nên OK vuông góc NP
\(\widehat{OKM}=\widehat{OAM}=\widehat{OBM}=90^0\)
=>O,K,A,M,B cùng thuộc 1 đường tròn

a: Xét tứ giác ACMO có
\(\widehat{CAO}+\widehat{CMO}=90^0+90^0=180^0\)
=>ACMO là tứ giác nội tiếp
=>A,C,M,O cùng thuộc một đường tròn
b: Xét (O) có
CA,CM là các tiếp tuyến
Do đó: CA=CM và OC là phân giác của góc AOM
Xét (O) có
DM,DB là các tiếp tuyến
Do đó: DM=DB và OD là phân giác của góc MOB
OC là phân giác của góc AOM
=>\(\widehat{AOM}=2\cdot\widehat{MOC}\)
Ta có: OD là phân giác của góc MOB
=>\(\widehat{MOB}=2\cdot\widehat{MOD}\)
Ta có: \(\widehat{AOM}+\widehat{MOB}=180^0\)(hai góc kề bù)
=>\(2\cdot\widehat{MOC}+2\cdot\widehat{MOD}=180^0\)
=>\(2\cdot\left(\widehat{MOC}+\widehat{MOD}\right)=180^0\)
=>\(2\cdot\widehat{COD}=180^0\)
=>\(\widehat{COD}=90^0\)
Xét ΔOCD vuông tại O có OM là đường cao
nên \(OM^2=MC\cdot MD\)
mà MC=CA và MD=DB
nên \(AC\cdot BD=OM=R^2\) không đổi
c: Gọi N là trung điểm của CD
Xét hình thang ACDB(AC//DB) có
O,N lần lượt là trung điểm của AB,CD
=>ON là đường trung bình của hình thang ABDC
=>ON//AC//BD
=>ON\(\perp\)AB
Vì ΔCOD vuông tại O có N là trung điểm của CD
nên N là tâm đường tròn ngoại tiếp ΔCOD
Xét (N) có
NO là bán kính
AB\(\perp\)NO tại O
Do đó: AB là tiếp tuyến của (N)
=>AB là tiếp tuyến của đường tròn ngoại tiếp ΔCOD

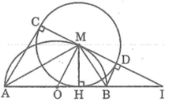
Trong đường tròn (M; MH), theo tính chất hai tiếp tuyến cắt nhau, ta có:
- MA là tia phân giác của góc HMC

Vậy C, M, D thẳng hàng.

a: ΔONP cân tại O
mà OK là đường trung tuyến
nên OK\(\perp\)NP tại K
Ta có: \(\widehat{OAM}=\widehat{OBM}=\widehat{OKM}=90^0\)
=>O,A,M,B,K cùng thuộc đường tròn đường kính OM
b: Xét (O) có
MA,MB là tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của BA(1)
OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO là đường trung trực của AB
=>MO\(\perp\)AB tại H và H là trung điểm của AB
Xét ΔOAM vuông tại A có AI là đường cao
nên \(OI\cdot OM=OA^2=R^2\)
Xét ΔOAM vuông tại A có AI là đường cao
nên \(OI\cdot IM=IA^2\)
c: AC\(\perp\)BM
OB\(\perp\)BM
Do đó: OB//AC
=>OB//AH
BD\(\perp\)MA
OA\(\perp\)MA
Do đó: BD//OA
=>BH//OA
Xét tứ giác OBHA có
OB//HA
OA//HB
Do đó: OBHA là hình bình hành
Hình bình hành OBHA có OB=OA
nên OBHA là hình thoi
d: OBHA là hình thoi
=>OH là đường trung trực của BA
mà M nằm trên đường trung trực của BA(cmt)
nên O,H,M thẳng hàng

a: Xét ΔOBA vuông tại B có BH là đường cao
nên OH*OA=OB^2=R^2
b: Xét ΔABC và ΔADB có
góc ABC=góc ADB
góc BAC chung
Do đó; ΔABCđồng dạng với ΔADB
=>AB/AD=AC/AB
=>AB^2=AD*AC
=>AD*AC=AH*AO

1. Xét nửa đường tròn (O) , có:
AC, CD là 2 tiếp tuyến của nửa đường tròn (O) (tiếp điểm A, D) (gt)
=> CA = CD , \(\widehat{CAO}=\widehat{CDO}=90^o\)
Xét tứ giác CAOD, có:
\(\widehat{CAO}+\widehat{CDO}=90^o+90^o=180^o\)
\(\widehat{CAO}\)và \(\widehat{CDO}\)là 2 góc đối nhau
=> ACDO là tứ giác nội tiếp
Xét \(\Delta CDM\)và \(\Delta CBD\), có:
\(\widehat{MCD}chung\)
\(\widehat{CDM}=\widehat{CBD}\)(góc nội tiếp và góc tạo bời tia tiếp tuyến và dây cung cùng chắn \(\widebat{MD}\) )
\(\Rightarrow\Delta~\Delta\left(gg\right)\)
\(\Rightarrow\frac{CD}{CB}=\frac{CM}{CD}\Leftrightarrow CD^2=CM.CB\)
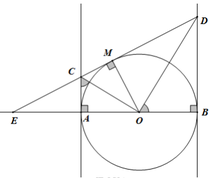

4) Ta có: \(AM//PQ\)( cùng vuông góc với OC )
Xét tam giác COQ có: \(EM//OQ\)
\(\Rightarrow\frac{CE}{CO}=\frac{EM}{OQ}\)( hệ quả của định lý Ta-let ) (1)
Xét tam giác COP có: \(AE//OP\)
\(\Rightarrow\frac{CE}{CO}=\frac{AE}{OP}\)( hệ quả của định lý Ta-let ) (2)
Từ (1) và (2) \(\Rightarrow\frac{EM}{OQ}=\frac{AE}{OP}\)Mà AE=EM
\(\Rightarrow OQ=OP\)
Xét tam giác CPQ và tam giác COP có chung đường cao hạ từ C, đáy \(OP=\frac{PQ}{2}\)
\(\Rightarrow S_{\Delta CPQ}=2.S_{\Delta COP}\)
Ta có: \(S_{\Delta COP}=\frac{1}{2}OA.CP=\frac{1}{2}R.CP\)
Áp dụng hệ thức lượng trong tam giác COP vuông tại O có đường cao OA ta có:
\(OA^2=CA.AP\)
Mà \(CA.AP\le\frac{\left(CA+AP\right)^2}{4}=\frac{PC^2}{4}\)( BĐT cô-si )
Dấu "=" xảy ra \(\Leftrightarrow AC=AP\)
\(\Rightarrow PC^2\ge4OA^2\)
\(\Rightarrow PC\ge2OA=2R\)
\(\Rightarrow S_{\Delta COP}\ge R^2\)
\(\Rightarrow S_{\Delta CPQ}\ge2R^2\)
Dấu "=" xảy ra \(\Leftrightarrow AC=AP\)
Mà tam giác COP vuông tại O có đường cao OA
\(\Rightarrow AC=AP=OA=R\)
Khi đó áp dụng định lý Py-ta-go vào tam giác CAO vuông tại A ta được:
\(AC^2+AO^2=OC^2\)
\(\Rightarrow OC=\sqrt{AC^2+AO^2}=R\sqrt{2}\)
Vậy điểm C thuộc đường thẳng d sao cho \(OC=R\sqrt{2}\)thì diện tích tam giác CPQ nhỏ nhất
giải hộ mik câu 4 nhé thanks