Có hai loại quặng sắt: quặng loại I và quặng loại II. Khối lượng tổng cộng của hai loại quặng là 10 tấn. Khối lượng sắt nguyên chất trong quặng loại I là 0,8 tấn, trong quặng loại II là 0,6 tấn. Biết tỉ lệ sắt nguyên chất trong quặng loại I nhiều hơn tỉ lệ sắt nguyên chất trong quặng loại II là 10%. Tính khối lượng của mỗi loại quặng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi khối lượng quặng loại 1 là x ( \(x\ne0\) )
Khối lượng quặng 2 là : \(10-x\left(tấn\right)\)
Tỉ lệ sắt nguyên chất trong quặng loại I là: \(\dfrac{0,8}{x}\)
Tỉ lệ sắt nguyên chất trong quặng loại II là: \(\dfrac{0,6}{10-x}\)
Do tỉ lệ sắt nguyên chất trong quặng loại I nhiều hơn tỉ lệ sắt nguyên chất trong quặng loại II là 10%
Nên ta có phương trình:
\(\dfrac{0,8}{x}-\dfrac{0,6}{10-x}=\dfrac{10}{100}\)
\(\Leftrightarrow0,8\left(10-x\right)-0,6x=0,1x\left(10-x\right)\)
\(\Leftrightarrow8\left(10-x\right)-6x=x\left(10-x\right)\)
\(\Leftrightarrow80-8x-6x=10x-x^2\)
\(\Leftrightarrow x^2-24x+80=0\)
\(\Leftrightarrow x\left(x-20\right)-4\left(x-20\right)=0\)
\(\Leftrightarrow\left(x-20\right).\left(x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-20=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=20\left(l\right)\\x=4\left(n\right)\end{matrix}\right.\)
Vậy: Khối lượng quặng loại I là 4 tấn, khối lượng quặng loại I là: 10 – 4 = 6 tấn.
Giúp câu này vứi ạk
Có hai loại quặng sắt, quặng loại 1 và loại II, tổng khối lượng là 12 tấn khối sắt nguyên chất trong quặng loại I là 1,8 tấn, trong quặng loại II là 1,6 tấn. Biết tỉ lệ sắt nguyên chất trong quặng loại 1 hơn tỉ lệ sắt nguyên chất trong quặng loại II là 10%. Tính khối lượng mỗi loại quặng.

70a + 40b = 60⇔
a + b
30a + 40 = 60⇔30a = 20 a + b ⇔10a = 20b⇔a = 2b
lại có
a − 8 + b − 2
70 a − 8 + 40 b − 2 = 58⇔
a − 8 + b − 2
30 a − 8 + 40 = 58⇔30 a − 8 = 18 a + b − 10
⇔30a − 240 = 18a + 18b − 180⇔12a − 18b = 60
thay a=2b vào phương trình trên ta có
12 × 2b − 18b = 60⇔24b − 18b = 60⇔6b = 60⇔b = 10⇒a = 20
Vậy khối lượng quặng 1 là 20 tấn
Gọi khối lượng quặng loại I và loại II lần lượt là x(tấn) và y(tấn).
Khi đó, do tổng khối lượng là 10 tấn nên
\(x+y=10\)
Tỉ lệ sắt nguyên chất trong quặng loại I là \(\frac{0,8}{x}\) và quặng loại II là \(\frac{0,6}{y}\)
Do tỉ lệ sắt nguyên chất trong quặng loại I hơn tỉ lệ sắt nguyên chất trong quặng loại II là 10% nên ta có
\(\frac{0,8}{x}-\frac{0,6}{y}=10\%=\frac{1}{10}\)
Vậy ta có hệ
\(\hept{\begin{cases}x+y=10\\\frac{0,8}{x}-\frac{0,6}{y}=\frac{1}{10}\end{cases}}\)
Từ ptrinh đầu ta suy ra y=10−x. Thế vào ptrinh sau ta có
\(\frac{0,8}{x}-\frac{0,6}{10-x}=\frac{1}{10}\)
\(\Leftrightarrow\frac{8}{x}-\frac{6}{10-x}=1\)
\(\Leftrightarrow8\left(10-x\right)-6x=x\left(10-x\right)\)
\(\Leftrightarrow x^2-24x+80=0\)
\(\Leftrightarrow\left(x-4\right)\left(x-20\right)=0\)
Vậy ta có x=4 hoặc x=20 (loại)
Suy ra y=6
Vậy khối lượng quặng loại I là 4 tấn, khối lượng quặng loại II là 6 tấn.

gọi x,y là số tấn quặng sắt loại I và loại II đã trộn với nhau lúc ban đầu
khi đó
phần trăm quặng sắt của hỗn hợp trên là \(\frac{0.7x+0.4y}{x+y}=0.6\)
phần trăm của quặng sắt của hỗn hợp sau là \(\frac{0.7\left(x+5\right)+0.4\left(y-5\right)}{x+5+y-5}=0.65\Leftrightarrow\frac{0.7x+0.4y+0.15}{x+y}=0.65\)
hay \(\frac{0.7x+0.4y}{x+y}+\frac{1.5}{x+y}=0.65\Rightarrow\frac{1.5}{x+y}=0.05\Rightarrow x+y=30\Rightarrow0.7x+0.4y=18\)
từ đây ta giải hệ \(\hept{\begin{cases}x+y=30\\0.7x+0.4y=18\end{cases}\Leftrightarrow\hept{\begin{cases}x=20\\y=10\end{cases}}}\)

Gọi khối lượng quặng loại thứ nhất là x ( tấn), loại thứ hai là y (tấn)
Điều kiện: x > 0; y > 0
Lượng sắt nguyên chất có trong mỗi loại quặng bằng lượng sắt có trong hỗn hợp ta có phương trình:
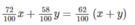
Thêm mỗi loại quặng 15 tấn ta được hỗn hợp chứa 63,25% sắt, ta có phương trình:
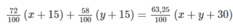
Ta có hệ phương trình:
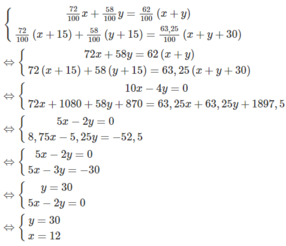
Cả hai giá trị x = 12; y = 30 thỏa mãn điều kiện bài toán.
Vậy loại quặng thứ nhất có 12 tấn, loại quặng thứ hai có 30 tấn.

Để cho ra quặng 66% thì cần trộn tỷ lệ quặng 75% : quặng 50% là 82/75 : 1 hay 82/75 : 75/75.
Như vậy để có 25 tấn quặng 66% thì cần:
Quặng 75%
(82 x 25) : (82 + 75)= 2075/157 tấn
Quặng 50%
(75 x25) :(82+75)= 1875/157 tấn

Gọi khối lượng mỗi quặng là a và b (tấn)
ta có: \(\frac{70a+40b}{a+b}=60\Leftrightarrow\frac{30a}{a+b}+40=60\Leftrightarrow30a=20\left(a+b\right)\Leftrightarrow10a=20b\Leftrightarrow a=2b\)
lại có\(\frac{70\left(a-8\right)+40\left(b-2\right)}{\left(a-8\right)+\left(b-2\right)}=58\Leftrightarrow\frac{30\left(a-8\right)}{a-8+b-2}+40=58\Leftrightarrow30\left(a-8\right)=18\left(a+b-10\right)\)
\(\Leftrightarrow30a-240=18a+18b-180\Leftrightarrow12a-18b=60\)
thay a=2b vào phương trình trên ta có
\(12\times2b-18b=60\Leftrightarrow24b-18b=60\Leftrightarrow6b=60\Leftrightarrow b=10\Rightarrow a=20\)
Vậy khối lượng quặng 1 là 20 tấn, khối lượng quặng 2 là 10 tấn

Gọi khối lượng của quặng loại I là x(tấn)
(Điều kiện: 0<x<=10)
Khối lượng của quặng loại II là 10-x(tấn)
Tỉ lệ sắt nguyên chất trong quặng loại I là \(\dfrac{0.8}{x}\left(tấn\right)\)
Tỉ lệ sắt nguyên chất trong quặng loại II là \(\dfrac{0.6}{10-x}\left(tấn\right)\)
Tỉ lệ sắt nguyên chất trong quặng loại I nhiều hơn tỉ lệ sắt nguyên chất trong quặng loại II là 10%=0,1 nên ta có;
\(\dfrac{0.8}{x}-\dfrac{0.6}{10-x}=0.1\)
=>\(\dfrac{8}{x}-\dfrac{6}{10-x}=1\)
=>\(\dfrac{8}{x}+\dfrac{6}{x-10}=1\)
=>\(\dfrac{8x-80+6x}{x\left(x-10\right)}=1\)
=>\(x\left(x-10\right)=14x-80\)
=>\(x^2-24x+80=0\)
=>(x-20)(x-4)=0
=>\(\left[{}\begin{matrix}x-20=0\\x-4=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=20\left(loại\right)\\x=4\left(nhận\right)\end{matrix}\right.\)
Vậy: Khối lượng quặng loại I là 4 tấn
Khối lượng quặng loại II là 10-4=6 tấn