C=4(X-2)MŨ2+6/6COS giá trị nhỏ nhất
C=4(x-2)mũ2+6/6 tìm giá trị nhỏ nhất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NH
0
TD
1
15 tháng 4 2022
\(\left(x+1\right)\left(x+2\right)>=\left(x-2\right)^2-1\)
\(\Leftrightarrow x^2+3x+2>=x^2-4x+4-1\)
=>3x+2>=-4x+3
=>7x>=1
hay x>=1/7
HY
1
AH
Akai Haruma
Giáo viên
16 tháng 7 2021
Lời giải:
a. Áp dụng BĐT Cô-si:
$x^4+9\geq 6x^2$
$y^4+9\geq 6y^2$
$\Rightarrow x^4+y^4+18\geq 6(x^2+y^2)$
$A+18\geq 36$
$A\geq 18$
Vậy GTNN của $A$ là $18$ khi $x^2=y^2=3$
b.
$(x-y)^2\geq 0$
$\Leftrightarrow x^2+y^2\geq 2xy$
$\Leftrightarrow 2(x^2+y^2)\geq (x+y)^2$
$\Leftrightarrow 12\geq (x+y)^2$
$\Rightarrow B=x+y\leq \sqrt{12}$. Vậy $B$ max bằng $\sqrt{12}$ khi $x=y=\sqrt{3}$
$(x-y)^2\geq 0$
$\Leftrightarrow x^2+y^2\geq 2xy$
$\Leftrightarrow 6\geq 2C$
$\Leftrightarrow C\leq 3$. Vậy $C_{\max}=3$. Giá trị này đạt tại $x=y=-\sqrt{3}$
LN
1
HM
1
MT
15 tháng 6 2015
1) tìm giá trị nhỏ nhất của M = x(x-4) + 13
M=x(x-4)+13=x2-4x+13
=x2-4x+4+9
=(x-2)2+9\(\ge\)9(vì (x-2)2\(\ge\)0)
Dấu "=" xảy ra khi x-2 =0
<=>x=2
Vậy giá trị nhỏ nhất của M là 9 tại x=2
2) tìm giá trị lớn nhất của P = x(10-x) +6
P = x(10-x) +6=10x-x2+6=-x2+10x-25+31
=-(x2-10x+25)+31
=-(x-5)2+31\(\le\)31(vì -(x-5)2\(\le\)0)
Dấu = xảy ra khi x-5=0
<=>x=5
vậy giá trị lớn nhất của P là 31 tại x=5
CM
18 tháng 2 2018
Ta có: 
+Vẽ đường thẳng y= x với x≥3 đi qua hai điểm O(0; 0) và A(1;1) và lấy phần đường thẳng bên phải của đường thẳng x= 3.
+Vẽ đường thẳng y=5x-12 với 2≤ x≤ 3 đi qua hai điểm B(3;3) và C( 2; -2) và lấy phần đường thẳng nằm giữa của hai đường thẳng x=2; x=3.
+Vẽ đường thẳng y= -x đi qua hai điểm O và D( -1; -1) và lấy phần đường thẳng bên trái của đường thẳng x= 2
+ Dựa vào đồ thị hàm số ta có:
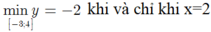
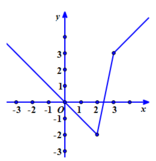
Chọn C.
15 tháng 9 2016
T/C của gttđ là >= 0 nên
a) GTNN = -4
b) GTLN = 2
c) GTNN = 2
Lời giải:
Ta thấy: $(x-2)^2\geq 0$ với mọi $x$
$\Rightarrow 4(x-2)^2+6\geq 6$
$\Rightarrow C=\frac{4(x-2)^2+6}{6}\geq 1$
Vậy $C$ có GTNN bằng 1. Giá trị này đạt được khi $x-2=0$
Hay $x=2$