Trong cùng 1 mặt phẳng tọa độ cho (d):y=-2x+k và (d'):y=\(\left(\sqrt{k+2}-5\right)x+3\left(k\ge-2\right)\). Tìm k để (d)//(d')
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1:
a: 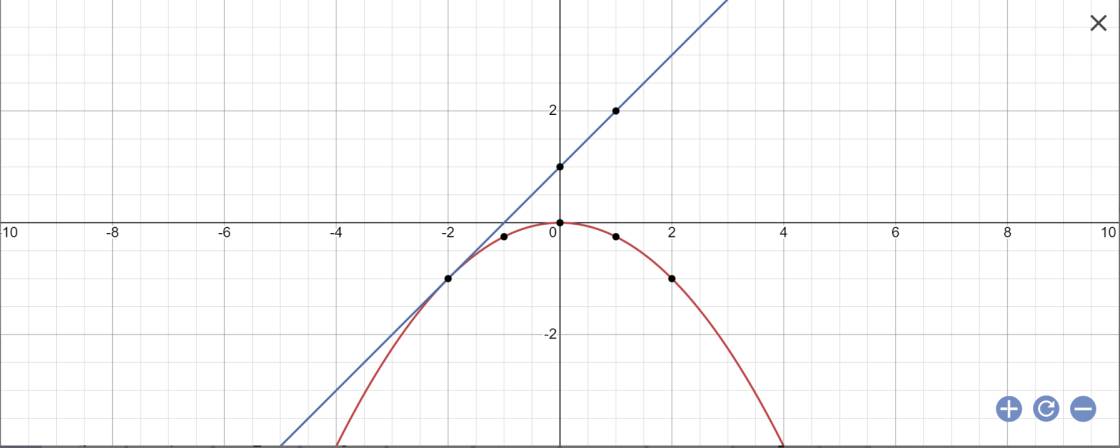
b: PTHĐGĐ là:
-1/4x^2-x-1=0
=>x^2+4x+4=0
=>(x+2)^2=0
=>x=-2
=>y=-1/4*(-2)^2=-1
2: 3x-y=5 và 2x+3y=18
=>9x-3y=15 và 2x+3y=18
=>11x=33 và 3x-y=5
=>x=3 và y=3*3-5=4

PTHĐGĐ là:
x^2-2x-m+2=0
Δ=(-2)^2-4(-m+2)
=4+4m-8=4m-4
Để (P) tiếp xúc (d) thì 4m-4=0
=>m=1
=>x^2-2x+1=0
=>x=1
=>y=1

PTHĐGĐ là:
x^2-2x-m+1=0
Δ=(-2)^2-4*1*(-m+1)
=4+4m-4=4m
Để (P) tiếp xúc (d) thì 4m=0
=>m=0
=>x^2-2x+1=0
=>x=1
=>y=1

\(b,\text{PT hoành độ giao điểm: }2x-5=-\dfrac{1}{2}x\Leftrightarrow\dfrac{5}{2}x=5\Leftrightarrow x=2\Leftrightarrow y=-1\Leftrightarrow M\left(2;-1\right)\)

a) Ta có: (d) \(y=2x-1\)
Hàm số cắt: \(Ox\left(\dfrac{1}{2};0\right);Oy\left(0;-1\right)\)
(d') \(y=x+1\)
Hàm số cắt: \(Ox\left(-1;0\right);Oy\left(0;1\right)\)
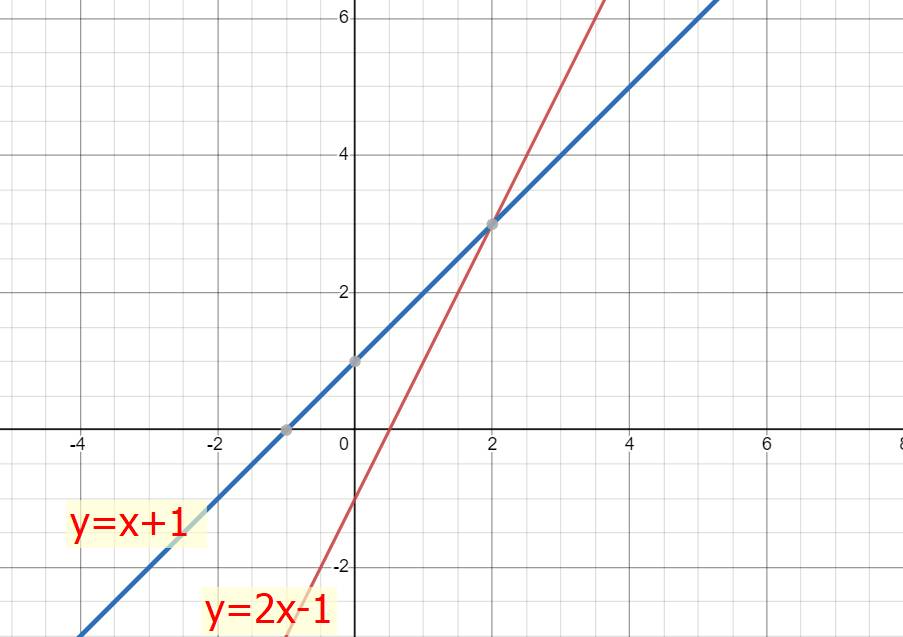
b) Phương trình hoành độ giao điểm cùa (d) và (d')
\(x+1=2x-1\)
\(\Leftrightarrow2x-x=1+1\)
\(\Leftrightarrow x=2\)
Thay x = 2 vào (d) ta có:
\(y=2\cdot2-1=3\)
Vậy tọa độ giao điểm của (d) và (d') là \(A\left(2;3\right)\)

b. PT hoành độ giao điểm \(x-3=2x+1\Leftrightarrow x=-4\Leftrightarrow y=-7\Leftrightarrow M\left(-4;-7\right)\)
Giúp mình vẽ hình với làm nốt mấy câu còn lại nữa
Mình cảm ơn

a: Thay x=10 vào (d1), ta được:
\(y=2\cdot10-1=20-1=19\)
=>A(10;19) thuộc (d1)
Thay x=-4 vào (d1), ta được:
\(y=2\left(-4\right)-1=-8-1=-9\)
=>B(-4;-7) không thuộc (d1)
Thay x=-11 vào (d1), ta được:
\(y=2\cdot\left(-11\right)-1=-22-1=-23\)
=>C(-11;-23) thuộc (d1)
b: 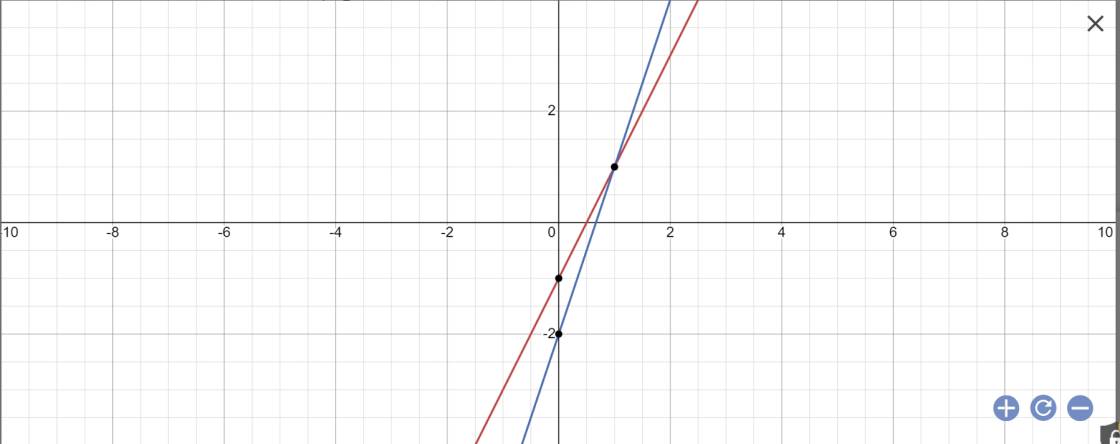
c: Tọa độ giao điểm của (d1) và (d2) là:
\(\left\{{}\begin{matrix}3x-2=2x-1\\y=2x-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x-2x=-1+2=1\\y=2x-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\cdot1-1=1\end{matrix}\right.\)
d: Để (d3) đồng quy với (d1),(d2) thì (d3) đi qua giao điểm của (d1) và (d2)
=>(d3) đi qua F(1;1)
Thay x=1 và y=1 vào (d3), ta được:
1(m-1)+3=1
=>m-1+3=1
=>m+2=1
=>m=-1

b, PT hoành độ giao điểm: \(2x-5=-\dfrac{1}{2}x\Leftrightarrow x=2\Leftrightarrow y=-\dfrac{1}{2}\cdot2=-1\)
\(\Leftrightarrow A\left(2;-1\right)\)
Vậy A(2;-1) là tọa độ giao điểm 2 đths
Để (d)//(d') thì
\(\left\{{}\begin{matrix}\sqrt{k+2}-5=-2\\k\ne3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\sqrt{k+2}=3\\k\ne3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}k+2=9\\k\ne3\end{matrix}\right.\)
=>k=7(nhận)