cho hình chóp S.ABC đáy là tam giác vuông (AB vuông BC) cạnh bên SA vuông góc với (ABC)
a) chứng minh BC vuông (SAB)
b) BH là đường cao tam giác ABC. Chứng minh BH vuông SC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 1
a.
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\BC\perp AC\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow BC\perp\left(SAC\right)\)
b.
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\\CK\in\left(ABC\right)\end{matrix}\right.\) \(\Rightarrow SA\perp CK\)
Theo gt: \(CK\perp AB\) (CK là đường cao)
\(\Rightarrow CK\perp\left(SAB\right)\)
Mà \(SB\in\left(SAB\right)\Rightarrow CK\perp SB\)
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 3 2023
A là khẳng định sai.
Vì \(SB\perp\left(ABC\right)\) nên \(SB\perp BC\)
Nếu \(SA\perp BC\Rightarrow SA||SB\) hoặc SA trùng SB (đều vô lý)
M
10 tháng 5 2021
Tự vẽ hình nhé:
a, Ta có: \(BC\perp AB\) (\(\Delta ABC\) vuông tại \(B\))
\(SA\perp BC\left(SA\perp\Delta ABC;BC\subset\left(ABC\right)\right)\)
\(AB\cap SA=\left\{A\right\}\)
\(AB,SA\subset\left(SAB\right)\)
\(\Rightarrow BC\perp\left(SAB\right)\)
b, Ta có \(BC\perp\left(SAB\right)\left(cmt\right)\)
mà \(SA\subset\left(SAB\right)\)
\(\Rightarrow BC\perp SA\)
15 tháng 6 2023
a: (SAB) và (SAC) cùng vuông góc (ABC)
(SAB) cắt (SAC)=SA
=>SA vuông góc (ABC)
b: SA vuông góc CH
CH vuông góc AB
=>CH vuông góc (SAB)
=>(SCH) vuông góc (SAB)
20 tháng 3 2023
a: BC vuông góc AM
BC vuông góc SA
=>BC vuông góc (SAM)
b: BC vuông góc (SAM)
=>BC vuông góc SM
=>(SM;(ABC))=90 độ
CM
9 tháng 10 2019
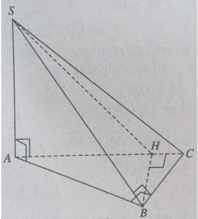
a) BC ⊥ SA & BC ⊥ AB) ⇒ BC ⊥ (SAB)
⇒ BC ⊥ SB.
⇒ tam giác SBC vuông tại B.
b) BH ⊥ AC & BH ⊥ SA ⇒ BC ⊥ (SAC)
⇒ (SBH) ⊥ (SAC).
c) d[B, (SAC)] = BH. Ta có:
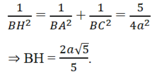
a.
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\BC\perp AB\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow BC\perp\left(SAB\right)\)
b.
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\\BH\in\left(ABC\right)\end{matrix}\right.\) \(\Rightarrow SA\perp BH\)
Lại có \(BH\perp AC\) (do BH là đường cao)
\(\Rightarrow BH\perp\left(SAC\right)\)
Mà \(SC\in\left(SAC\right)\)
\(\Rightarrow BH\perp SC\)