Giải
bài toán theo hệ thức Vi-ét
giúp mình với ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H
26 tháng 12 2022
\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.2^{32}}\)
Ta lấy vễ trên chia vế dưới
\(=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}\)
Ta lấy vế trên chia vế dưới
\(=2^3.3=24\)
S
26 tháng 12 2022
\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.3^{32}}=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}=2^3.3=8.3=24\)
15 tháng 3 2023
28:
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
b: Xet ΔBCA vuông tại A có AH là đường cao
nên AH^2=HB*HC
c: Xét tứ giác AMHN có
góc AMH=góc ANH=góc MAN=90 độ
=>AMHN là hình chữ nhật
=>O là trung điểm của AH
=>\(S_{COA}=S_{COH}\)
d: AM/AB+AN/AC
\(=\dfrac{AM\cdot AB}{AB^2}+\dfrac{AN\cdot AC}{AC^2}\)
\(=AH^2\left(\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\right)=AH^2\cdot\dfrac{1}{AH^2}=1\)
NV
2
10 tháng 4 2022
Câu 9: A
Câu 10: C
Câu 11: C
Câu 12: A
Câu 13; B
Câu 14: C
NV
1
NV
1
7 tháng 11 2021
#include <bits/stdc++.h>
using namespace std;
double a,cv,dt;
int main()
{
cin>>a;
cv=a*4;
dt=a*a;
cout<<fixed<<setprecision(2)<<cv<<endl;
cout<<fixed<<setprecision(2)<<dt;
return 0;
}
3 tháng 12 2021
#include <bits/stdc++.h>
using namespace std;
double a,b,cv,dt;
int main()
{
cin>>a>>b;
cv=(a+b)*2;
dt=a*b;
cout<<fixed<<setprecision(2)<<cv<<endl;
cout<<fixed<<setprecision(2)<<dt;
return 0;
}
DH
1
29 tháng 3 2018
Phương trình 5x2 + 2x -16 =0 có hệ số a=5 ,b=2 c=-16
Ta có: Δ'=12 -5(-16) = 1 + 80 =81 >0
Δ' = 81 =9
Phương trình 3x2 -2x -5 =0 có hệ số a =3,b = -2, c = -5
Ta có: Δ'=(-1)2 -3(-5) = 1 + 15 =16 >0
Δ' = 16 =4
Phương trình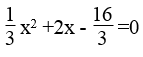 
⇔ x2 +6x – 16 = 0 có hệ số a = 1, b = 6, c = -16
Δ'=32 -1(-16) = 9 +16 =25 > 0
Δ' = 25 =5
Phương trình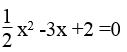 
⇔ x2 -6x +4 =0 có hệ số a=1,b=-6,c=4
Ta có: Δ'=(-3)2 -1.4 = 9 -4 =5 >0
Δ' = 5
Thay x=1 vào pt ta được pt ẩn m: 1-2(m-1).1+m=0
<=> 1 - 2m + 2 + m = 0
<=> m=3
Thay m=3 vào pt đầu và được: x2 - 4x + 3 = 0
<=> x2 - x - 3x + 3 =0
<=> x(x-1) - 3(x-1)=0
<=> (x-3) (x-1)=0
<=> x-3=0 hoặc x-1=0
<=> x=3 hoặc x=1
Vậy: Khi x=1 thì m=3, nghiệm còn lại của pt là x=3