Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi G là trọng tâm của tam giác SAD và M là điểm thuộc cạnh BC sao cho GM// (SCD). Khi đó tỉ số diện tích của hai tam giác MAB và MAC là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn D
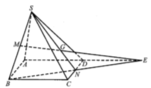
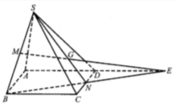
Gọi N là trung điểm của CD, khi đó MG, BN, AD đồng quy tại E.
Do AB = 2ND nên ND là đường trung bình của tam giác EAB ⇒ D là trung điểm của AE

Đáp án A
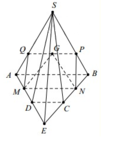
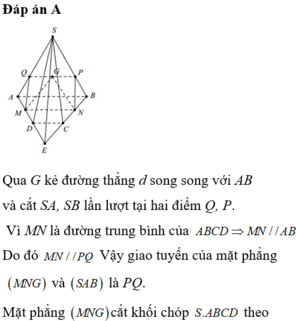
Qua G kẻ đường thẳng d song song với AB và cắt SA, SB lần lượt tại hai điểm Q, P. Vì MN là đường trung bình của ABCD ⇒ MN//AB
Do đó MN//PQ. Vậy giao tuyến của mặt phẳng (MNG) và (SAB) là PQ.
Mặt phẳng (MNG) cắt khối chóp S.ABCD theo thiết diện là tứ giác MNPQ
Vì MN//PQ suy ra MNPQ là hình thang
Để MNPQ là hình bình hành ⇔ MN=PQ (1)
Gọi I là trung điểm của AB, G là trọng tâm tam giác S A B ⇒ S G S I = 2 3
Tam giác SAB có P Q / / A B ⇒ P Q A B = S G S I = 2 3 ⇔ P Q = 2 3 A B (2)
Mà MN là đường trung bình hình thang A B C D ⇒ M N = A B + C D 2 (3)
Từ (1) , (2) và (3) suy ra 2 3 A B = A B + C D 2 ⇔ 4 A B = 3 A B + 3 C D ⇔ A B = 3 C D .

a) S là điểm chung của hai mặt phẳng (SAB) và (SCD) mà AB // CD
Từ S kẻ Sx sao cho Sx // AB // CD nên Sx là giao tuyến của hai mặt phẳng (SAB) và (SCD).
b) Gọi E là trung điểm của AB
G là trọng tâm tam giác SAB nên \(\frac{{EG}}{{SE}} = \frac{1}{3}\)
N là trọng tâm tam giác ABC nên\(\frac{{EN}}{{EC}} = \frac{1}{3}\)
Theo Ta lét, suy ra GN // SC mà SC \( \subset \) (SAC). Do đó, GN // (SAC)

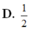



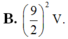
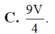
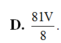


Gọi F là trung điểm SD \(\Rightarrow\dfrac{GF}{GA}=\dfrac{1}{2}\) theo t/c trọng tâm
Trong mp (SAD), qua G kẻ đường thẳng song song SD cắt AD tại E
\(\Rightarrow GE||SD\Rightarrow GE||\left(SCD\right)\)
\(\left\{{}\begin{matrix}GM||\left(SCD\right)\\GE||\left(SCD\right)\end{matrix}\right.\) \(\Rightarrow\left(GME\right)||\left(SCD\right)\Rightarrow ME||\left(SCD\right)\Rightarrow ME||CD\)
\(\Rightarrow CDEM\) là hình bình hành (2 cặp cạnh đối song song)
\(\Rightarrow MC=ED\Rightarrow MB=EA\)
Áp dụng định lý Talet trong tam giác ADF: \(\dfrac{ED}{EA}=\dfrac{GF}{GA}=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{MC}{MB}=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{S_{MAB}}{S_{MAC}}=\dfrac{MB}{MC}=2\)