Trên hình bình hành abcd tâm o lấy m n sao cho vecto am=vecto mb vectoan=2vectond.gọi k h lần lượt là trung điểm mn oc biểu diễn kh theo vecto ad ab
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 9 2020
a) N trung điểm AD \(\Rightarrow AN=\frac{AD}{2}=\frac{BC}{2}\)
M trung điểm BC \(\Rightarrow MC=\frac{BC}{2}\Rightarrow AN=MC\)mà AN//MC
nên AMCN là hình bình hành \(\Rightarrow\overrightarrow{AM}=\overrightarrow{NC}\)
b) Tương tự câu a ta được \(\hept{\begin{cases}ND=BM=\frac{1}{2}BC\\ND//BM\end{cases}}\)=> NDMB là hình bình hành=> NB//DM (1)
Xét 2 tam giác ANI và NDK: \(\hept{\begin{cases}AN=ND=\frac{AD}{2}\\\widehat{NAI}=\widehat{DNK}\left(AM//NC\right)\\\widehat{ANI}=\widehat{NDK}\left(NB//MD\right)\end{cases}\Rightarrow\Delta ANI=\Delta NDK\left(g.c.g\right)}\)
\(\Rightarrow NI=DK\)(2)
(1), (2) => \(\overrightarrow{NI}=\overrightarrow{DK}\)
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 9 2021
\(\overrightarrow{NC}=2\overrightarrow{ND}=2\overrightarrow{NC}+2\overrightarrow{CD}\Rightarrow\overrightarrow{NC}=2\overrightarrow{DC}\Rightarrow\overrightarrow{CN}=2\overrightarrow{CD}\)
a.
\(\overrightarrow{DM}=\overrightarrow{DC}+\overrightarrow{CM}=\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{CB}=\overrightarrow{AB}-\dfrac{1}{2}\overrightarrow{AD}\)
\(\overrightarrow{MN}=\overrightarrow{MC}+\overrightarrow{CN}=\dfrac{1}{2}\overrightarrow{BC}+2\overrightarrow{CD}=-2\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AD}\)
b.
\(\left\{{}\begin{matrix}\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}\\\overrightarrow{BD}=\overrightarrow{BA}+\overrightarrow{AD}=-\overrightarrow{AB}+\overrightarrow{AD}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\dfrac{1}{2}\overrightarrow{AC}-\dfrac{1}{2}\overrightarrow{BD}\\\overrightarrow{AD}=\dfrac{1}{2}\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{BD}\end{matrix}\right.\)
\(\Rightarrow\overrightarrow{MN}=-2\left(\dfrac{1}{2}\overrightarrow{AC}-\dfrac{1}{2}\overrightarrow{BD}\right)+\dfrac{1}{2}\left(\dfrac{1}{2}\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{BD}\right)=-\dfrac{3}{4}\overrightarrow{AB}+\dfrac{5}{4}\overrightarrow{BD}\)
14 tháng 11 2021
\(a,\overrightarrow{AB}-\overrightarrow{DA}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{0}=\overrightarrow{AD}\)
\(b,\overrightarrow{AM}=\dfrac{\overrightarrow{AO}+\overrightarrow{AB}}{2}=\dfrac{\overrightarrow{AB}}{2}+\dfrac{\dfrac{1}{2}\overrightarrow{AC}}{2}=\overrightarrow{\dfrac{AB}{2}}+\dfrac{1}{4}\overrightarrow{AC}\)
\(=\overrightarrow{\dfrac{AB}{2}}+\dfrac{\overrightarrow{AB}+\overrightarrow{BC}}{4}=\dfrac{3}{4}\overrightarrow{AB}+\dfrac{\overrightarrow{BC}}{4}=\dfrac{1}{4}\overrightarrow{BC}+\dfrac{3}{4}\overrightarrow{AB}\left(1\right)\)
\(\overrightarrow{AN}=\overrightarrow{BN}-\overrightarrow{BA}=k.\overrightarrow{BC}+\overrightarrow{AB}\left(2\right)\)
\(\left(1\right)\left(2\right)A,M,N\) \(thẳng\) \(hàng\Leftrightarrow\dfrac{k}{\dfrac{1}{4}}=\dfrac{1}{\dfrac{3}{4}}\Leftrightarrow k=\dfrac{1}{3}\)
AH
Akai Haruma
Giáo viên
26 tháng 8 2021
Lời giải:
a.
$\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}$ (tính chất hình bình hành)
b.
$\overrightarrow{AM}=\frac{2}{3}\overrightarrow{AC}=\frac{2}{3}(\overrightarrow{AB}+\overrightarrow{AD})$
c.
$\overrightarrow{AN}=\overrightarrow{AC}+\overrightarrow{CN}=\overrightarrow{AC}+\frac{1}{2}\overrightarrow{BA}$
$=\overrightarrow{AB}+\overrightarrow{AD}-\frac{1}{2}\overrightarrow{AB}$
$=\frac{1}{2}\overrightarrow{AB}+\overrightarrow{AD}$
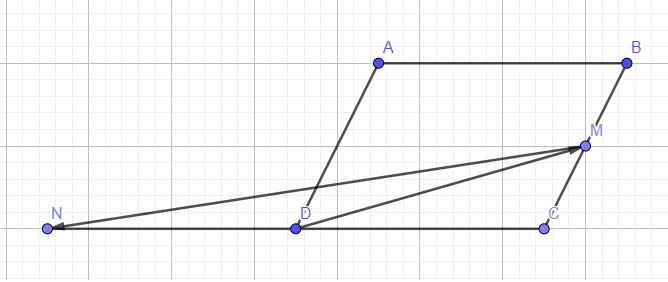
\(\overrightarrow{AM}=\overrightarrow{MB}=\overrightarrow{MA}+\overrightarrow{AB}=-\overrightarrow{AM}+\overrightarrow{AB}\Rightarrow2\overrightarrow{AM}=\overrightarrow{AB}\Rightarrow\overrightarrow{AM}=\dfrac{1}{2}\overrightarrow{AB}\)
\(\overrightarrow{AN}=2\overrightarrow{ND}=2\left(\overrightarrow{NA}+\overrightarrow{AD}\right)=-2\overrightarrow{AN}+2\overrightarrow{AD}\Rightarrow3\overrightarrow{AN}=2\overrightarrow{AD}\Rightarrow\overrightarrow{AN}=\dfrac{2}{3}\overrightarrow{AD}\)
Do K là trung điểm MN
\(\Rightarrow\overrightarrow{AK}=\dfrac{1}{2}\left(\overrightarrow{AM}+\overrightarrow{AN}\right)=\dfrac{1}{2}\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AD}\right)=\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AD}\)
Theo tính chất hbh: \(\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}\)
Do O là tâm hình bình hành \(\Rightarrow\overrightarrow{AO}=\overrightarrow{OC}=\dfrac{1}{2}\overrightarrow{AC}\)
Mà H là trung điểm OC \(\Rightarrow\overrightarrow{OH}=\dfrac{1}{2}\overrightarrow{OC}=\dfrac{1}{4}\overrightarrow{AC}\)
\(\Rightarrow\overrightarrow{AH}=\overrightarrow{AO}+\overrightarrow{OH}=\dfrac{1}{2}\overrightarrow{AC}+\dfrac{1}{4}\overrightarrow{AC}=\dfrac{3}{4}\overrightarrow{AC}=\dfrac{3}{4}\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{AD}\)
\(\Rightarrow\overrightarrow{KH}=\overrightarrow{KA}+\overrightarrow{AH}=-\overrightarrow{AK}+\overrightarrow{AH}\)
\(=-\dfrac{1}{4}\overrightarrow{AB}-\dfrac{1}{3}\overrightarrow{AD}+\dfrac{3}{4}\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{AD}=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{5}{12}\overrightarrow{AD}\)
\(\overrightarrow{AN}=2\overrightarrow{ND}\)
=>A,N,D thẳng hàng và AN=2ND
ABCD là hình bình hành tâm O
=>O là trung điểm chung của AC và BD
H là trung điểm của OC
nên HO=HC=1/2CO
=>\(HO=HC=\dfrac{1}{2}\cdot\dfrac{1}{2}\cdot CA=\dfrac{1}{4}CA\)
\(\overrightarrow{AM}=\overrightarrow{MB}\)
=>AM=MB và M nằm giữa A và B
=>M là trung điểm của AB
AN+ND=AD
=>2ND+ND=AD
=>AD=3ND
=>AN/AD=2/3
=>\(\overrightarrow{AN}=\dfrac{2}{3}\cdot\overrightarrow{AD}\)
\(\overrightarrow{KH}=\overrightarrow{KM}+\overrightarrow{MH}\)
\(=\dfrac{1}{2}\overrightarrow{NM}+\overrightarrow{MB}+\overrightarrow{BC}+\overrightarrow{CH}\)
\(=\dfrac{1}{2}\left(\overrightarrow{NA}+\overrightarrow{AM}\right)+\dfrac{1}{2}\overrightarrow{AB}+\overrightarrow{BC}+\dfrac{1}{4}\overrightarrow{CA}\)
\(=\dfrac{1}{2}\left(-\dfrac{2}{3}\overrightarrow{AD}+\dfrac{1}{2}\overrightarrow{AB}\right)+\dfrac{1}{2}\overrightarrow{AB}+\overrightarrow{AD}+\dfrac{1}{4}\left(\overrightarrow{CD}+\overrightarrow{CB}\right)\)
\(=-\dfrac{1}{3}\overrightarrow{AD}+\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AB}+\overrightarrow{AD}-\dfrac{1}{4}\overrightarrow{AB}-\dfrac{1}{4}\overrightarrow{AD}\)
\(=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{5}{12}\overrightarrow{AD}\)