Cho tam giác ABC vuông tại A, đường cao AH,kẻ HI ⊥ AB tại I, HK ⊥ AC tại K.Trên tia HI lấy điểm D sao cho DI=IH trên tia HK lấy điểm E sao cho EK=KH.C/m
a.Tứ giác AIHK là hình gì?
b.Kẻ trung tuyến AM biết AB =12 cm,AC=16cm.Tính AM
c.BC=BD+CE
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác AIHK có
HK//AI
HI//AK
Do đó: AIHK là hình bình hành
mà \(\widehat{KAI}=90^0\)
nên AIHK là hình chữ nhật

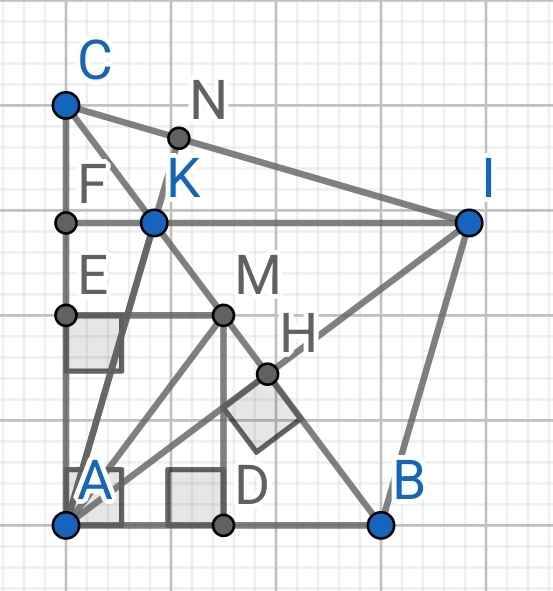
a) Tứ giác ADME có:
∠AEM = ∠ADM = ∠EAD = 90⁰ (gt)
⇒ ADME là hình chữ nhật
b) Do HI = HA (gt)
⇒ H là trung điểm của AI
Do HK = HB (gt)
⇒ H là trung điểm của BK
Tứ giác ABIK có:
H là trung điểm của AI (cmt)
H là trung điểm của BK (cmt)
⇒ ABIK là hình bình hành
⇒ IK // AB
Mà AB ⊥ AC (∆ABC vuông tại A)
⇒ IK ⊥ AC
⇒ IK là đường cao của ∆ACI
Lại có:
AH ⊥ BC (do AH là đường cao của ∆ABC)
⇒ CH ⊥ AI
⇒ CH là đường cao thứ hai của ∆ACI
∆ACI có:
IK là đường cao (cmt)
CH là đường cao (cmt)
⇒ AK là đường cao thứ ba của ∆ACI
⇒ AK ⊥ IC

a: Xét tứ giác ADME có
\(\widehat{ADM}=\widehat{AEM}=\widehat{DAE}=90^0\)
=>ADME là hình chữ nhật
b: Xét tứ giác ABKI có
M là trung điểm chung của AK và BI
Do đó: ABKI là hình bình hành
=>KI//AB
mà AB\(\perp\)AC
nên KI\(\perp\)AC
Xét ΔCAI có
IK,CH là đường cao
IK cắt CH tại K
Do đó: K là trực tâm của ΔCAI
=>AK\(\perp\)IC

a: Xét ΔAEH có
AB vừa là đường cao, vừa là trung tuyến
=>ΔAEH cân tại A
=>AE=AH
b: Xét ΔAHF có
AC vừa là đường cao, vừa là trung tuyến
=>ΔAHF cân tại A
=>AH=AF=AE

a) Tam giác ADI và AHI có
AI cạnh chung
AID=AIH=90 độ
ID=IH(gt)
vậy tam giác ADI=AHI(c.g.c)
b) xét tam giác BID và BIH có
BI cạnh chung
BID=BIH=90 độ
ID=IH(gt)
vậy tam giác BID=BIH(c.g.c)
=>DBI=HBI(góc tuognư ứng
xét tam giác ABD và ABH có
DAB=HAB( vì tam giác AID=AIH)
AB cạnh chung
DBA=HBA(cmt)
vậy tam giác ABD=ABH(g.c.g)
=> ADB=AHB=90 độ
hay AD vuông góc với BD.
c)BC=HB+HC=9+16=25(cm)
Áp dụng định lí pi-ta-go vào tam giác ABH, ta có
\(AB^2=AH^2+HB^2=AH^2+9^2=AH^2+81\)
Áp dụng định lí pi-ta-go vào tam giác ACH, ta có
\(AC^2=AH^2+HC^2=AH^2+16^2=AH^2+256\)
Áp dụng định lí pi-ta-go vào tam giác ACH, ta có
\(BC^2=AB^2+AC^2\)
hay \(25^2=AH^2+81+AH^2+256\)
\(625=2AH^2+337\)
\(2AH^2=625-337=288\)
\(AH^2=\frac{288}{2}=144\)
\(AH=\sqrt{144}=12\left(cm\right)\).

a) dien h tam giac ABC la :S ABC =1/2 AB * AC = 1/2* 6 *8 = 24(m2)
b) Tu giac AIHK co :
goc AIH = goc HKA = goc KAI = 90 do
suy ra AIKH la hinh chu nhat
c)Tu giac AHMD co :
AK = KM
KH=KD
suy ra AHMD la hinh binh hanh
ma goc HKC = 90 do
suy ra AHMD la hinh thoi
c) Trong tam AHC vuong tai H co :
KH la trung tuyen
suy ra KH = 1/2 AC
Chung minh tuong tu ta co : HI = 1/2 AB
De IHKA la hinh vuong thi IH = HK
ma IH = 1/2 AB
KH = 1/2 AC
suy ra AB = AC
suy ra tam giac ABC can
ma tam giac ABC vuong(gt)
suy ra tam giac ABC vuong can
Vay tam giac ABC vuong can thi AIHK la hinh vuong

Bài 2
gọi E là trung điểm của KB
Vì tam giác CKB có BM=MC ; BE=EK
=>EM//KC
Vì tam giác ENM có AN=AM ; KA//EM
=>EK=KN
Vì KN=KE=EB=>NK=1/2KB
a: Xét tứ giác AIHK có
\(\widehat{AIH}=\widehat{AKH}=\widehat{KAI}=90^0\)
=>AIHK là hình chữ nhật
b: Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=12^2+16^2=400\)
=>BC=20(cm)
ΔABC vuông tại A có AM là đường trung tuyến
nên \(AM=\dfrac{1}{2}BC=\dfrac{1}{2}\cdot20=10\left(cm\right)\)
c: Xét ΔBHD có
BI là đường cao
BI là đường trung tuyến
Do đó: ΔBHD cân tại B
=>BH=BD
Xét ΔCEH có
CK là đường cao
CK là đường trung tuyến
Do đó: ΔCEH cân tại C
=>CH=CE
BC=BH+CH
mà BH=BD và CH=CE
nên BC=BD+CE
a. Tứ giác AIHK là hình vuông.
Vì tam giác ABC vuông tại A, nên đường cao AH cũng là đường trung tuyến của tam giác ABC. Do đó, AH cắt BC thành hai đoạn bằng nhau, tức là BH = CH.
Vì DI = IH và EK = KH, nên ta có DI = IH = EK = KH.
Do đó, AI = AH + IH = AH + DI = AH + EK = AK.
Vậy tứ giác AIHK là hình vuông.
b. Kẻ trung tuyến AM biết AB = 12 cm, AC = 16 cm. Ta cần tính AM.
Trung tuyến AM chia đôi đoạn BC, nên BM = MC.
Áp dụng định lý Pythagoras trong tam giác vuông ABC, ta có:
AB^2 + AC^2 = BC^2
12^2 + 16^2 = BC^2
144 + 256 = BC^2
400 = BC^2
BC = √400
BC = 20 cm
Vì BM = MC, nên BM = MC = BC/2 = 20/2 = 10 cm.
Vậy AM = AB + BM = 12 + 10 = 22 cm.
c. BC = BD + CE
Vì DI = IH và EK = KH, nên BD = DI và CE = EK.
Do đó, BC = BD + CE = DI + EK = DI + KH = DI + IH = DI + DI = 2DI.
Vậy DI = BC/2.