Giúp mình bài này với. có công thức tổng quát nhé! 3 tik cho ng đầu tiên.
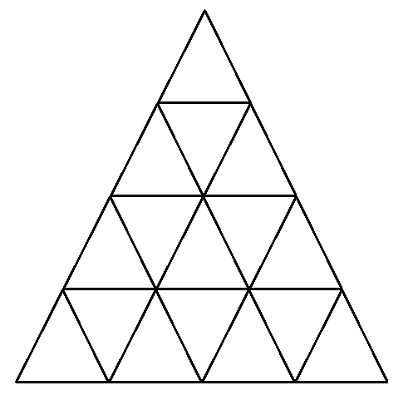
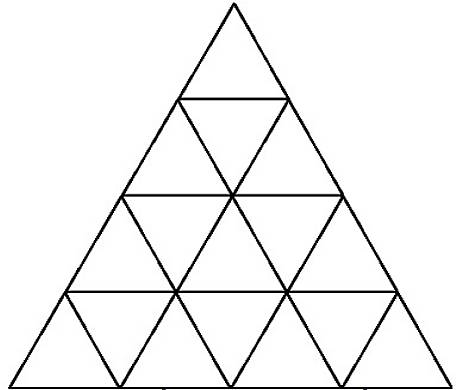
Tháp tam giác là hình tam giác đều lớn cấu thành từ nhiều tam giác với nhiều tầng. Hỏi tháp tam giác với độ cao là 19 có bao nhiêu hình thang cân. Ví dụ:
- Tháp tam giác độ cao là 2 có 3 hình thang cân.
- Tháp tam giác có độ cao là 3 có 18 hình thang cân.


Theo như ảnh thì b học toán MTCT nên đầu tiên ta tìm ra quy luật rồi chỉ việc bấm máy!!!
Ta có: Với độ cao là 1 => số tam giác là: 1
Với độ cao là 2 => số tam giác là: (1+3)+1
Với độ cao là 3 => số tam giác là: (1+3+5)+(1+2)+1
Với độ cao là 4 => số tam giác là: (1+3+5+7)+(1+2+3)+(1+2)+1
Với độ cao là 5 => số tam giác là: (1+3+5+7+9)+(1+2+3+4)+(1+2+3)+(1+2)+1
Từ đây có thể suy ra quy luật => với độ cao là 244 thì số tam giác là:
(1+3+...+487)+(1+2+...+243)+(1+2+...+242)+...+(1+2)+1=(487+1)∗2442+244∗2432+243∗2422+...+3∗22+2∗12(487+1)∗2442+244∗2432+243∗2422+...+3∗22+2∗12
=59536+243∑1x(x+1)2∑1243x(x+1)2
=59536+2421090
=2480626
Bài viết đã được chỉnh sửa nội dung bởi Sergio BusBu: 21-12-2015 - 17:46Kira Tatsuya yêu thích