Một xe chuyển động chậm dần đều với tốc độ đầu 10m/s. Trong giây thứ 6 xe đi được 1,25m. Tính quãng đường xe đi được đến khi dừng lại. Chỉ mình zới, mình làm ra gia tốc nó số lẻ nên nghi ngờ:") Hết coin gòi, cảm ơn nhiều.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

15 tháng 7 2019
1)
v0=0
Sgiây thứ 3 = 5m \(\Leftrightarrow S_{giâythứ3}=v_0t+\frac{1}{2}at^2-v_0\left(t-1\right)-\frac{1}{2}a\left(t-1\right)^2=v_0+a\left(t-\frac{1}{2}\right)=0+a\left(3-\frac{1}{2}\right)=\frac{5}{2}a\)
=> \(\frac{5}{2}a=5\)
=> a =2\(m/s^2\)
Quãng đường xe đi được sau 10s là:
t =10s => \(s=v_0t+\frac{1}{2}at^2=\frac{1}{2}.2.10^2=100\left(m\right)\)

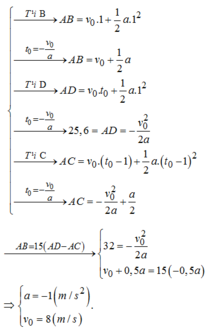

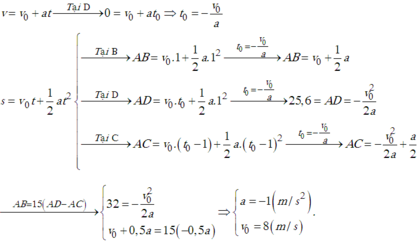


Dữ kiện đầu đề cho giây thứ 6 xe đi được 1,25 m chứ không phải là 6 giây đầu xe đi được 1,25m.
Nên mình làm kiểu:
Chọn chiều dương là chiều chuyển động của xe.
Quãng đường trong giây thứ 6:\(\Delta s_6=s_6-s_5\Leftrightarrow1,25=v_06+\dfrac{1}{2}a.6^2-v_0.5-\dfrac{1}{2}a.5^2\Rightarrow a=-1,59m/s^2\)
Áp dụng \(2ad=v^2-v_0\Rightarrow s=d\approx31,45m\)
Á chị =0
Gia tốc xe: \(S=v_0t+\dfrac{1}{2}at^2\)
\(\Rightarrow1,25=10\cdot6+\dfrac{1}{2}a\cdot6^2\)
\(\Rightarrow a=-\dfrac{235}{72}m/s^2\)
Quãng đường xe đi đến khi dừng lại: \(v^2-v_0^2=2aS'\)
\(\Rightarrow S'=\dfrac{v^2-v_0^2}{2a}=\dfrac{0-10^2}{2\cdot\left(-\dfrac{235}{72}\right)}=\dfrac{720}{47}m\approx15m\)