 e dag cần gấp a🥲
e dag cần gấp a🥲
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(VP=a^3+b^3+c^3-3bac\)
\(=\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc\)
\(=\left(a+b+c\right)\left[\left(a+b\right)^2-c\left(a+b\right)+c^2\right]-3ab\left(a+b+c\right)\)
\(=\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2-3ab\right)\)
\(=\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ac\right)=VT\)
b: \(VT=\left(3a+2b-1\right)\left(a+5\right)-2b\left(a-2\right)\)
\(=3a^2+15a+2ab+10b-a-5-2ab+4b\)
\(=3a^2+14a+14b-5\)
\(VP=\left(3a+5\right)\left(a+3\right)+2\left(7b-10\right)\)
\(=3a^2+9a+5a+15+14b-20\)
\(=3a^2+14a+14b-5\)
=>VT=VP
c: \(VT=a\left(b-x\right)+x\left(a+b\right)\)
\(=ab-ax+ax+bx\)
\(=ab+bx=b\left(a+x\right)=VP\)
d: \(VT=a\left(b-c\right)-b\left(a+c\right)+c\left(a-b\right)\)
\(=ab-ac-ab-bc+ca-cb\)
\(=-2bc\)
=VP



a, Vì AC⊥AB và BD⊥AB nên AC//BD
b, Vì AC//BD nên \(\widehat{D_1}=\widehat{ACD}\) (so le trong)
Mà \(\widehat{ACD}+\widehat{C_1}=180^0\left(kề.bù\right)\Rightarrow\widehat{ACD}=\widehat{D_1}=180^0-70^0=110^0\)


Gọi vận tốc xe 1 và xe 2 lần lượt là a,b
Theo đề, ta có:
1/4a=1/3b và 1,6(a+b)=112
=>a=40; b=30

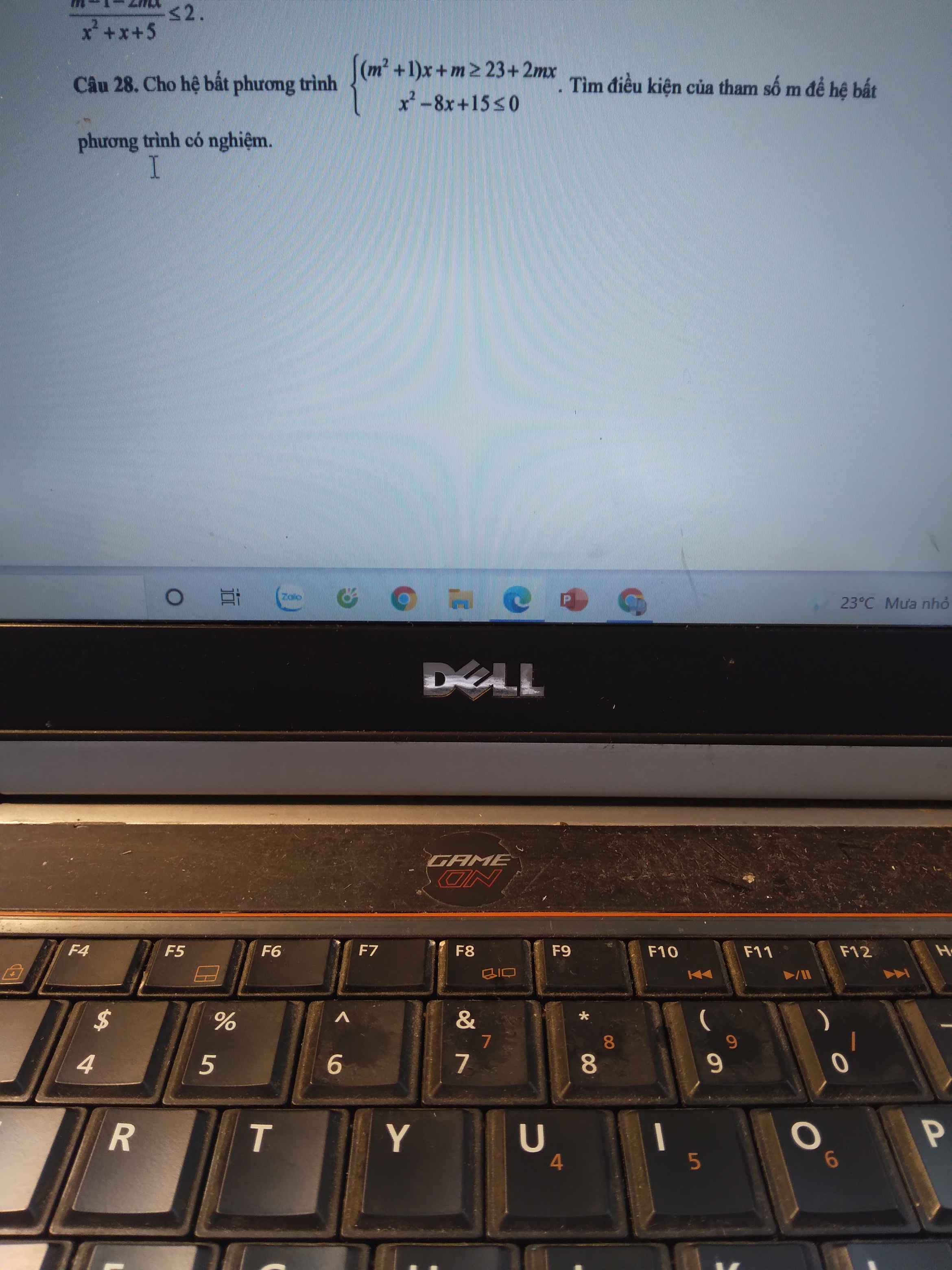
Xét BPT: \(x^2-8x+15\le0\Leftrightarrow3\le x\le5\Rightarrow D_1=\left[3;5\right]\)
Xét BPT: \(\left(m^2+1\right)x+m\ge23+2mx\)
\(\Leftrightarrow\left(m^2-2m+1\right)x\ge23-m\)
\(\Leftrightarrow\left(m-1\right)^2x\ge23-m\) (1)
- Với \(m=1\Rightarrow\left(1\right)\) trở thành \(0\ge22\) (vô lý) \(\Rightarrow\left(1\right)\) vô nghiệm (loại)
- Với \(m\ne1\Rightarrow\left(m-1\right)^2>0;\forall m\)
\(\left(1\right)\Leftrightarrow x\ge\dfrac{23-m}{\left(m-1\right)^2}\) \(\Rightarrow D_2=\left[\dfrac{23-m}{(m-1)^2};+\infty \right)\)
Hệ đã cho có nghiệm khi và chỉ khi \(D_1\cap D_2\ne\varnothing\)
\(\Rightarrow\dfrac{23-m}{\left(m-1\right)^2}\le5\)
\(\Leftrightarrow23-m\le5\left(m-1\right)^2\)
\(\Leftrightarrow5m^2-9m-18\ge0\Rightarrow\left[{}\begin{matrix}m\ge3\\m\le-\dfrac{6}{5}\end{matrix}\right.\)

\(A=\dfrac{1}{5}+\dfrac{1}{10}+\dfrac{1}{20}+\dfrac{1}{40}+\dfrac{1}{80}+\dfrac{1}{160}\\ A=\dfrac{35}{160}+\dfrac{16}{160}+\dfrac{8}{160}+\dfrac{4}{160}+\dfrac{2}{160}+\dfrac{1}{160}\\ A=\dfrac{66}{160}\\ A=\dfrac{33}{80}.\)

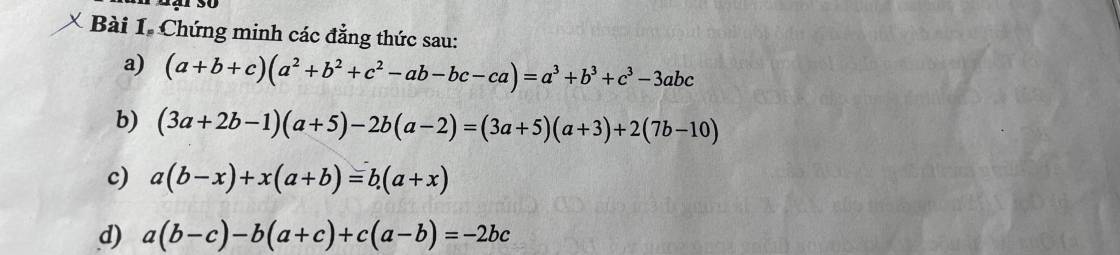



 dag cần gấp ạ! e c.ơn
dag cần gấp ạ! e c.ơn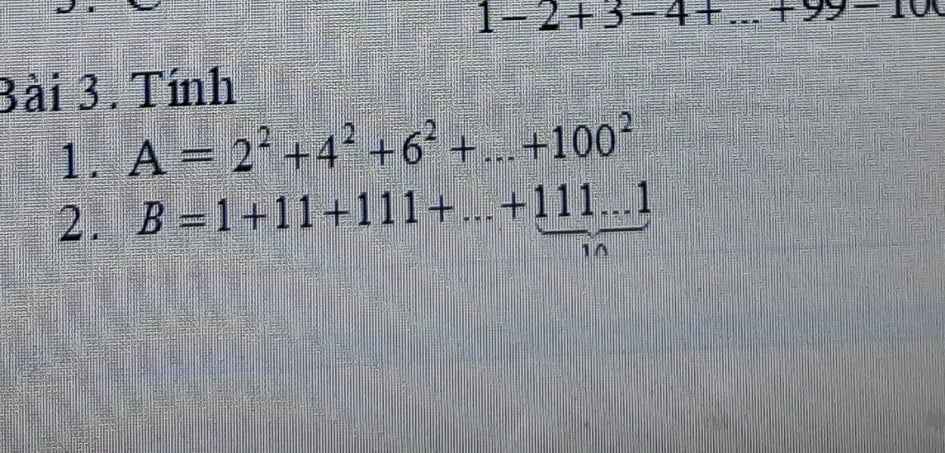 giúp em câu a. E tsu dag cần gấp mng giúp em với. Em cảm ơn
giúp em câu a. E tsu dag cần gấp mng giúp em với. Em cảm ơn

2 True
3 False
4 True
5 False
b
1 It is located on top of a hill
2 They were used to protect people inside the castle
3 They can go upstairs on narrow staircases
4 15000 people visit the castle each day