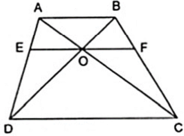
Cho hình thang(AB//CD) có O là giao điểm 2 đường chéo.Qua O kẻ đường thẳng song song với AB cắt BC lần lượt tại E và H.Chứng minh OE=OH. Giúp mình với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét ΔOAB và ΔOCD có
\(\widehat{OAB}=\widehat{OCD}\)(hai góc so le trong, AB//CD)
\(\widehat{AOB}=\widehat{COD}\)
Do đó: ΔOAB đồng dạng với ΔOCD
=>\(\dfrac{OA}{OC}=\dfrac{OB}{OD}\)
=>\(\dfrac{OC}{OA}=\dfrac{OD}{OB}\)
=>\(\dfrac{OC}{OA}+1=\dfrac{OD}{OB}+1\)
=>\(\dfrac{OC+OA}{OA}=\dfrac{OD+OB}{OB}\)
=>\(\dfrac{AC}{OA}=\dfrac{BD}{OB}\)
=>\(\dfrac{AO}{AC}=\dfrac{BO}{BD}\)(1)
Xét ΔADC có OE//DC
nên \(\dfrac{OE}{DC}=\dfrac{AO}{AC}\left(2\right)\)
Xét ΔBDC có OH//DC
nên \(\dfrac{OH}{DC}=\dfrac{BO}{BD}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\dfrac{OE}{DC}=\dfrac{OH}{DC}\)
=>OE=OH

Xét ΔADC có OE//DC
nên \(\dfrac{OE}{DC}=\dfrac{AE}{AD}\left(1\right)\)
Xét ΔBDC có OH//DC
nên \(\dfrac{OH}{DC}=\dfrac{BH}{BC}\left(2\right)\)
Xét hình thang ABCD có EH//AB//CD
nên \(\dfrac{AE}{ED}=\dfrac{BH}{HC}\)
=>\(\dfrac{ED}{AE}=\dfrac{CH}{HB}\)
=>\(\dfrac{ED+AE}{AE}=\dfrac{CH+HB}{HB}\)
=>\(\dfrac{AD}{AE}=\dfrac{CB}{HB}\)
=>\(\dfrac{AE}{AD}=\dfrac{BH}{BC}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\dfrac{OE}{DC}=\dfrac{OH}{DC}\)
=>OE=OH
Ta có \( \mathrm{OE} = \frac{1}{2}(\mathrm{AC} - \mathrm{BD}) \) và \( \mathrm{OH} = \frac{1}{2}(\mathrm{AC} - \mathrm{BD}) \).
Vì \( \mathrm{AB} / / \mathrm{CD} \), nên các tam giác \( \mathrm{ABE} \) và \( \mathrm{CDH} \) đồng dạng.
Do đó, \( \frac{\mathrm{AE}}{\mathrm{AD}} = \frac{\mathrm{CH}}{\mathrm{CD}} \).
Tương tự, \( \frac{\mathrm{BE}}{\mathrm{BA}} = \frac{\mathrm{CH}}{\mathrm{CD}} \).
Tổng hai phương trình trên ta có \( \frac{\mathrm{AE}+\mathrm{BE}}{\mathrm{AD}+\mathrm{BA}} = \frac{\mathrm{CH}}{\mathrm{CD}} \).
Nhưng \( \mathrm{AD}+\mathrm{BA} = \mathrm{AD}+\mathrm{BC} = \mathrm{AC} \) và \( \mathrm{AE}+\mathrm{BE} = \mathrm{AE}+\mathrm{AD} = \mathrm{DE} \).
Vậy \( \frac{\mathrm{DE}}{\mathrm{AC}} = \frac{\mathrm{CH}}{\mathrm{CD}} \) hoặc \( \mathrm{DE} = \frac{\mathrm{CH} \cdot \mathrm{AC}}{\mathrm{CD}} \).
Lưu ý rằng \( \mathrm{CH} \) là độ dài đoạn thẳng vuông góc từ \( \mathrm{C} \) đến \( \mathrm{AB} \), nên \( \mathrm{CH} = \frac{\mathrm{CD} \cdot \mathrm{BH}}{\mathrm{BC}} \).
Do đó, \( \mathrm{DE} = \frac{\mathrm{CD} \cdot \mathrm{BH} \cdot \mathrm{AC}}{\mathrm{BC} \cdot \mathrm{CD}} \).
Hóa giản và ta có \( \mathrm{DE} = \frac{\mathrm{BH} \cdot \mathrm{AC}}{\mathrm{BC}} \).
Xét tam giác \( \mathrm{BHE} \), ta thấy \( \mathrm{OE} \) là đoạn trung bình của \( \mathrm{BH} \), nên \( \mathrm{OE} = \frac{1}{2}\mathrm{BH} \).
Tổng kết lại, \( \mathrm{OE} = \frac{1}{2} \cdot \frac{\mathrm{BH} \cdot \mathrm{AC}}{\mathrm{BC}} = \frac{\mathrm{DE}}{2} = \mathrm{OH} \).
Vậy, chúng ta đã chứng minh được \( \mathrm{OE} = \mathrm{OH} \).

a: OM//CD
=>OM/CD=AO/AC=AM/AD
ON//DC
=>ON/CD=BO/BD=BN/BC
b: OM/CD=ON/CD(AM/AD=BN/BC)
=>OM=ON
c: 2/MN=1/AB+1/CD
=>2/MN=1/4+1/6=3/12+2/12=5/12
=>MN/2=12/5
=>MN=24/5=4,8cm

Áp dụng hệ quả của định lí Ta – lét cho OE//DC,
OF//DC và AB//DC ta được:
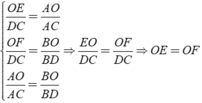
Điều phải chứng minh.

Áp dụng hệ quả của định lí Ta – lét cho OE//DC,
OF//DC và AB//DC ta được:
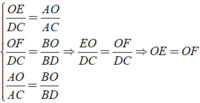
Điều phải chứng minh.

a: Xét ΔOAB và ΔOCD có
\(\widehat{OAB}=\widehat{OCD}\)(hai góc so le trong, AB//CD)
\(\widehat{AOB}=\widehat{COD}\)(hai góc đối đỉnh)
Do đó: ΔOAB\(\sim\)ΔOCD
=>\(\dfrac{OA}{OC}=\dfrac{OB}{OD}\)
=>\(\dfrac{OC}{OA}=\dfrac{OD}{OB}\)
=>\(\dfrac{OC}{OA}+1=\dfrac{OD}{OB}+1\)
=>\(\dfrac{OC+OA}{OA}=\dfrac{OD+OB}{OB}\)
=>\(\dfrac{AC}{OA}=\dfrac{BD}{OB}\)
=>\(\dfrac{OA}{AC}=\dfrac{OB}{BD}\)(2)
b: Xét ΔCAD có OE//AD
nên \(\dfrac{DE}{DC}=\dfrac{AO}{AC}\)(1)
Xét ΔBDC có OF//BC
nên \(\dfrac{CF}{CD}=\dfrac{BO}{BD}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\dfrac{DE}{DC}=\dfrac{CF}{CD}\)
=>DE=CF
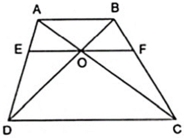
Giúp minh với
Sửa đề: lần lượt cắt AD,BC tại E và H
Xét ΔADC có OE//DC
nên \(\dfrac{OE}{DC}=\dfrac{AE}{AD}\left(1\right)\)
Xét ΔBDC có OH//DC
nên \(\dfrac{OH}{DC}=\dfrac{BH}{BC}\left(2\right)\)
Xét hình thang ABCD có EH//AB//CD
nên \(\dfrac{AE}{ED}=\dfrac{BH}{HC}\)
=>\(\dfrac{ED}{EA}=\dfrac{CH}{HB}\)
=>\(\dfrac{ED+EA}{EA}=\dfrac{CH+HB}{HB}\)
=>\(\dfrac{AD}{EA}=\dfrac{CB}{HB}\)
=>\(\dfrac{AE}{AD}=\dfrac{BH}{BC}\left(3\right)\)
Từ (1),(2),(3) suy ra OE=OH