Cho tam giác ABC vuônh tại A (AB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 4 2022
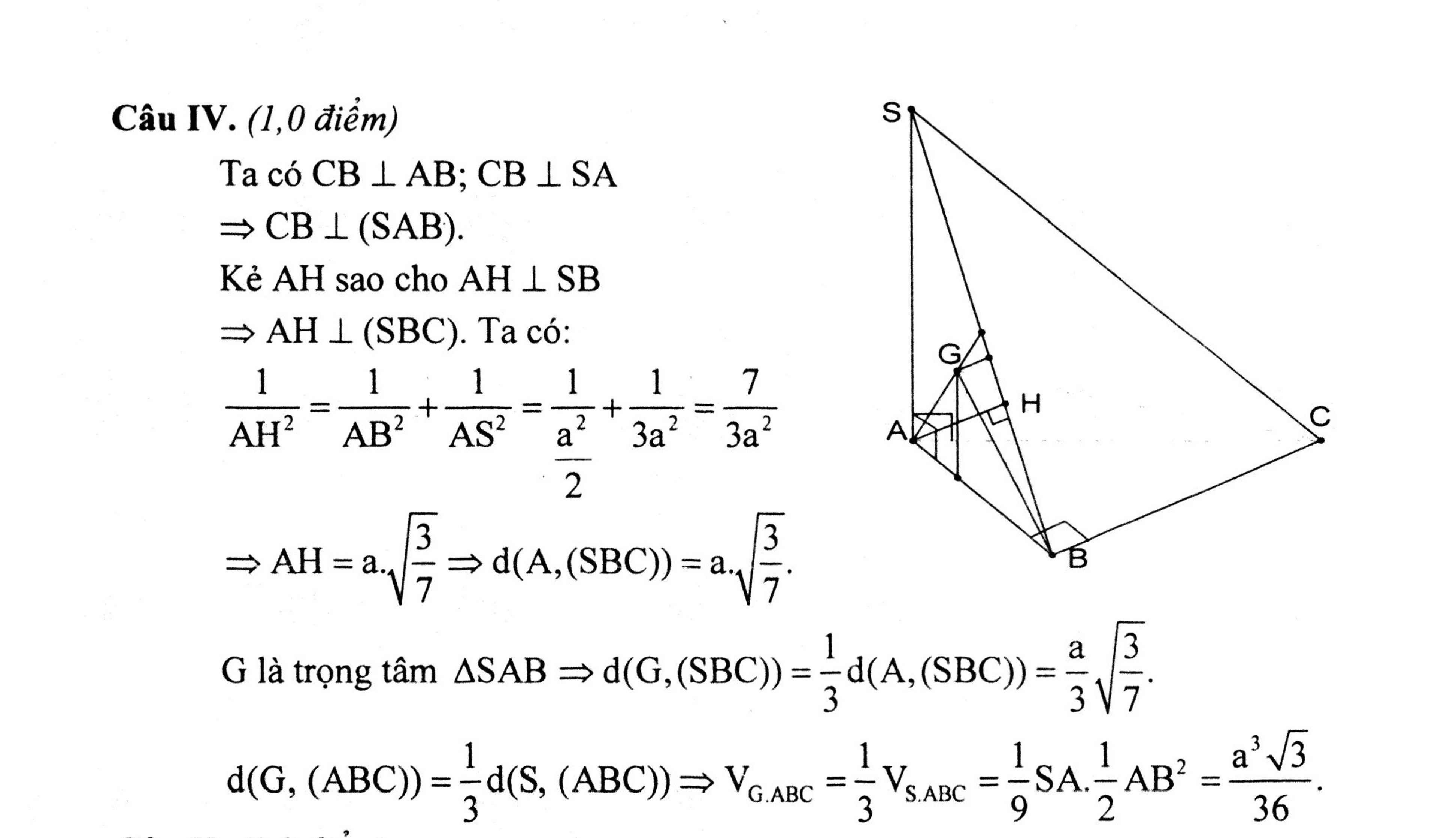
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\AB\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\Rightarrow BC=d\left(C;\left(SAB\right)\right)\)
Gọi D là trung điểm AB, theo tính chất trọng tâm: \(GD=\dfrac{1}{3}CD\)
\(\Rightarrow d\left(G;\left(SAB\right)\right)=\dfrac{1}{3}d\left(C;\left(SAB\right)\right)=\dfrac{1}{3}BC=\dfrac{1}{3}AB=\dfrac{a}{3}\)
6 tháng 4 2023
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
=>ΔAHB=ΔAHC
b: ΔABC cân tại A
mà AH là trung tuyến
nên AH là phân giác
c: Xet ΔAEH vuôngtại E và ΔAFH vuông tại F có
AH chung
góc EAH=góc FAH
=>ΔAEH=ΔAFH
=>AE=AF
=>ΔAEF cân tại A
mà AI là phân giác
nên AI là trung tuyến
3 tháng 12 2023
a: Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
=>ADHE là hình chữ nhật
b: ADHE là hình chữ nhật
=>AD//HE và AD=HE; AE//HD và AE=HD
AE=HD
A\(\in\)EF
Do đó: HD//AF
AE=HD
AE=AF
Do đó: HD=AF
Xét tứ giác AHDF có
AF//DH
AF=DH
Do đó: AHDF là hình bình hành
c:
AC và AF là hai tia đối nhau
mà E\(\in\)AC
nên AE và AF là hai tia đối nhau
=>A nằm giữa E và F
mà AE=AF
nên A là trung điểm của EF
Xét tứ giác EBFM có
A là trung điểm chung của EF và BM
nên EBFM là hình bình hành
Hình bình hành EBFM có EF\(\perp\)BM
nên EBFM là hình thoi
2 tháng 12 2021
\(1,HC=\dfrac{AH^2}{BH}=\dfrac{256}{9}\\ \Rightarrow AB=\sqrt{BH\cdot BC}=\sqrt{\left(\dfrac{256}{9}+9\right)9}=\sqrt{337}\\ 2,BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\\ \Rightarrow BH=\dfrac{AB^2}{BC}=6,4\left(cm\right)\\ 3,AC=\sqrt{BC^2-AB^2}=9\\ \Rightarrow CH=\dfrac{AC^2}{BC}=5,4\\ 4,AC=\sqrt{BC\cdot CH}=\sqrt{9\left(6+9\right)}=3\sqrt{15}\\ 5,AC=\sqrt{BC^2-AB^2}=4\sqrt{7}\left(cm\right)\\ \Rightarrow AH=\dfrac{AB\cdot AC}{BC}=3\sqrt{7}\left(cm\right)\\ 6,AC=\sqrt{BC\cdot CH}=\sqrt{12\left(12+8\right)}=4\sqrt{15}\left(cm\right)\)