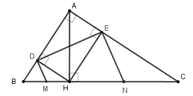
cho tam giác ABC vuông tại A, đường cao AH. Gọi E,F lần lượt là hình chiếu vuông góc của H trên các cạnh AB, AC. tính độ dài hf biết ab=sáu cm bc=10cm và bh =3,sáu(làm nhanh hộ mik vs ạ)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 12 2023
a: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
=>AEHF là hình chữ nhật
=>AH=EF
b: Ta có: ΔABH vuông tại H
=>\(HA^2+HB^2=AB^2\)
=>\(HA^2=6^2-3,6^2=23,04\)
=>\(HA=\sqrt{23,04}=4,8\left(cm\right)\)
Xét ΔHAB vuông tại H có HE là đường cao
nên \(AE\cdot AB=AH^2\)
=>\(AE\cdot6=4,8^2=23,04\)
=>\(AE=\dfrac{23.04}{6}=3,84\left(cm\right)\)
AEHF là hình chữ nhật
=>AE=HF
mà AE=3,84cm
nên HF=3,84cm
13 tháng 10 2022
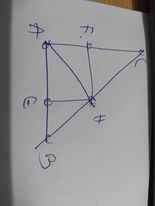
a: \(AB=\sqrt{3\cdot15}=3\sqrt{5}\left(cm\right)\)
\(AC=\sqrt{12\cdot15}=6\sqrt{5}\left(cm\right)\)
b: \(\dfrac{HF}{HE}=\dfrac{AE}{AF}=\dfrac{AH^2}{AB}:\dfrac{AH^2}{AC}=\dfrac{AC}{AB}=2\)
=>HF=2HE
AH
Akai Haruma
Giáo viên
20 tháng 12 2023
Lời giải:
a/ Tứ giác $AEHF$ có 3 góc vuông: $\widehat{A}=\widehat{E}=\widehat{F}=90^0$ nên là hình chữ nhật.
$\Rightarrow AH=EF$
b/ $HF=AE$ (do $AEHF$ là hcn)
Xét tam giác $AEH$ và $AHB$ có:
$\widehat{A}$ chung
$\widehat{AEH}=\widehat{AHB}=90^0$
$\Rightarrow \triangle AEH\sim \triangle AHB$ (g.g)
$\Rightarrow \frac{AE}{AH}=\frac{AH}{AB}$
$\Rightarrow AE=\frac{AH^2}{AB}=\frac{AB^2-BH^2}{AB}=\frac{6^2-3,6^2}{6}=3,84$ (cm)
CM
24 tháng 6 2019
Tứ giác AEHD là hình chữ nhật vì: A ^ = E ^ = D ^ = 90 o nên DE = AH.
Xét ABC vuông tại A có: A H 2 = HB.HC = 9.16 = 144 => AH = 12
Nên DE = 12cm
Đáp án cần chọn là: A
CM
22 tháng 10 2019
Tứ giác ARHD là hình chữ nhật vì: A ^ = E ^ = D ^ = 90 ∘ nên DE = AH.
Xét ∆ ABC vuông tại A có A H 2 = HB.HC = 4.9 = 36 ⇔ AH = 6
Nên DE = 6cm
Đáp án cần chọn là : D
15 tháng 10 2021
b: Xét ΔAHB vuông tại H có HD là đường cao ứng với cạnh huyền AB
nên \(AD\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HE là đường cao ứng với cạnh huyền AC
nên \(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AD\cdot AB=AE\cdot AC\)
hay \(\dfrac{AD}{AC}=\dfrac{AE}{AB}\)
Xét ΔADE vuông tại A và ΔACB vuông tại A có
\(\dfrac{AD}{AC}=\dfrac{AE}{AB}\)
Do đó: ΔADE\(\sim\)ΔACB
Suy ra: \(\widehat{ADE}=\widehat{ACB}\)
23 tháng 10 2021
a, Áp dụng HTL: \(BC=\dfrac{AB^2}{BH}=18\left(cm\right)\)
Áp dụng PTG: \(AC=\sqrt{BC^2-AB^2}=9\sqrt{3}\left(cm\right)\)
Áp dụng HTL: \(AH=\dfrac{AB\cdot AC}{BC}=\dfrac{9\cdot9\sqrt{3}}{18}=\dfrac{9\sqrt{3}}{2}\left(cm\right)\)
b, Áp dụng HTL: \(\left\{{}\begin{matrix}AB\cdot AE=AH^2\\AC\cdot AF=AH^2\end{matrix}\right.\Rightarrow AB\cdot AE=AC\cdot AF\)
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{AF}{AE}\)
Mà góc A chung nên \(\Delta AEF\sim\Delta ACB\left(c.g.c\right)\)
Do đó \(\widehat{AEF}=\widehat{ACB}\)