Bài 11: Cho nửa đường tròn tâm O đường kính C . Gọi Cx, Dy là các tia vuông góc với CD (Cx,Dy và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ CD). Qua M thuộc nửa đường tròn (M khác C và D), kẻ tiếp tuyến với nửa đường tròn nó cắt Cx và Dy theo thứ tự ở A và B. Chứng minh rằng: A,Góc AOB=9O độB, AB = CA+DBC, Tính CA.DB ko đổi khi điểm M di chuyển trên nửa đường tròn...
Đọc tiếp
Bài 11:
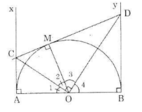
Cho nửa đường tròn tâm O đường kính C . Gọi Cx, Dy là các tia vuông góc với CD (Cx,Dy và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ CD). Qua M thuộc nửa đường tròn (M khác C và D), kẻ tiếp tuyến với nửa đường tròn nó cắt Cx và Dy theo thứ tự ở A và B. Chứng minh rằng:
A,Góc AOB=9O độ
B, AB = CA+DB
C, Tính CA.DB ko đổi khi điểm M di chuyển trên nửa đường tròn
SOS
a: Xét (O) có
AM,AC là tiếp tuyến
Do đó: AM=AC và OA là tia phân giác của \(\widehat{MOC}\)
=>\(\widehat{MOC}=2\cdot\widehat{MOA}\)
Xét (O) có
BM,BD là tiếp tuyến
Do đó: BM=BD và OB là phân giác của \(\widehat{MOD}\)
=>\(\widehat{MOD}=2\cdot\widehat{MOB}\)
\(\widehat{MOC}+\widehat{MOD}=180^0\)(hai góc kề bù)
=>\(2\cdot\widehat{MOA}+2\cdot\widehat{MOB}=180^0\)
=>\(2\left(\widehat{MOA}+\widehat{MOB}\right)=180^0\)
=>\(\widehat{MOA}+\widehat{MOB}=\dfrac{180^0}{2}=90^0\)
=>\(\widehat{AOB}=90^0\)
b: AB=AM+BM
mà AM=AC và BM=BD
nên AB=AC+BD
c: Xét ΔOAB vuông tại O có OM là đường cao
nên \(AM\cdot MB=OM^2\)
=>\(AC\cdot BD=R^2\) không đổi khi M di chuyển trên (O)