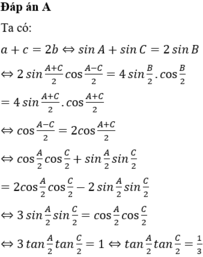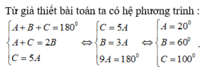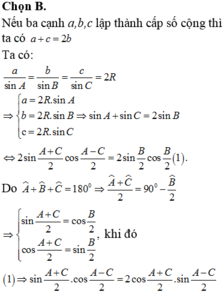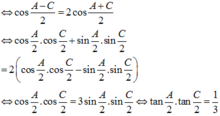Cho tam giác ABC có A=90°, a, √6/3, b, c theo thứ tự lập thành cấp số nhân. Tam giác ABC là tam giác có đặc điểm gì
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 4 2016
Theo giả thiết ta có hệ : \(\begin{cases}A=90^0\\a,b,\frac{\sqrt{6}}{3},c\end{cases}\)\(\Leftrightarrow\begin{cases}a^2=b^2+c^2\\\frac{2}{3}b^2=ac\Leftrightarrow b^2=\frac{3}{2}ac\end{cases}\)
Từ đó suy ra \(a^2=\frac{3}{2}ac+c^2\Leftrightarrow2a^2=3ac+2c^2\Leftrightarrow\left(2a+c\right)\left(a-2c\right)=0\)
\(\Rightarrow a=2c\left(2a+c>0\right)\)
Mà \(\cos B=\frac{c}{a}=\frac{1}{2}\Rightarrow B=60^0,C=30^0\)
Vậy tam giác ABC là tam giác nửa đều
CM
1 tháng 8 2017
Chọn D
Theo tính chất cấp số nhân, Ta có: ac=2/3 b2. Theo hệ thức lượng trong tam giác vuông, Ta có: b=a.sinB, c=a.cosB. vậy Ta có
CM
30 tháng 11 2018
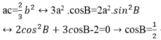
Theo giả thiết AB=AC, BC,AH,AB lập thành cấp số nhân nên ta có hệ:
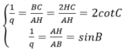
Từ đó ta có kết quả sau: 2cotC = sinC ⇔ 2cosC =sin2C = 1-cos2C
⇔ cos2C + 2cosC -1 =0 ⇒cosC = -1 +√2 (0° < C < 90°)
Do C là góc nhọn nên :
Cho nên công bội của cấp số nhân là:
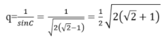
Đáp án C.
CM
11 tháng 9 2019
Chọn A.
Ta có: a + c = 2b ⇔ sinA + sinC = 2sinB
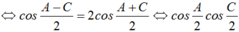
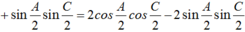
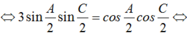
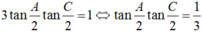
Do đó x + y = 4.
24 tháng 11 2017
a,Xét tam giác BDC:
Ta có: \(\hept{\begin{cases}gócD=90^0\\BM=MC\end{cases}\Rightarrow DM=\frac{1}{2}BC}\) (1)
Xét tam giác BEC:
Ta có: \(\hept{\begin{cases}gócE=90^0\\BM=MC\end{cases}\Rightarrow EM=\frac{1}{2}BC}\) (2)
Từ (1) và (2): \(\Rightarrow EM=MD=\frac{1}{2}BC\)
Suy ra: tam giác EMD là tam giác cân.
Lại có: N là trung điểm của tam giác can EMD.
Hay: N là đường cao của tam giác EMD
Vậy MN vuông góc với ED
b,Bó tay
CM
24 tháng 9 2017
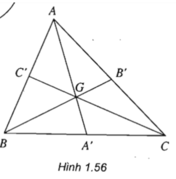
Theo đề bài ta có: AA', BB', CC' là các đường trung tuyến của ΔABC ⇒ G là trọng tâm
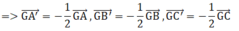
Vậy phép vị tự tâm G, tỉ số k = -1/2 biến tam giác ABC thành tam giác A'B'C'
