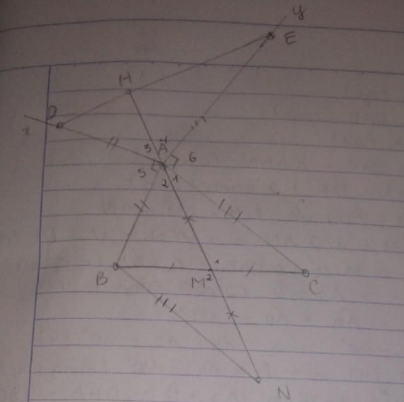
Vẽ hình sau: Cho ΔABC, góc A < 90o. Trên nửa mặt phẳng bờ là AB không chứa điểm C, vẽ tia Ax ⊥ AB và lấy trên Ax điểm D sao cho AD = AB. Trên nửa mặt phẳng bờ AC không chứa B, vẽ tia Ay ⊥ AC và lấy điểm E sao cho AE = AC. Chứng minh:
a) BE = CD.
b) BE ⊥ CD
c) Lấy M; N là trung điểm BE; DC. Chứng minh AM = AN.

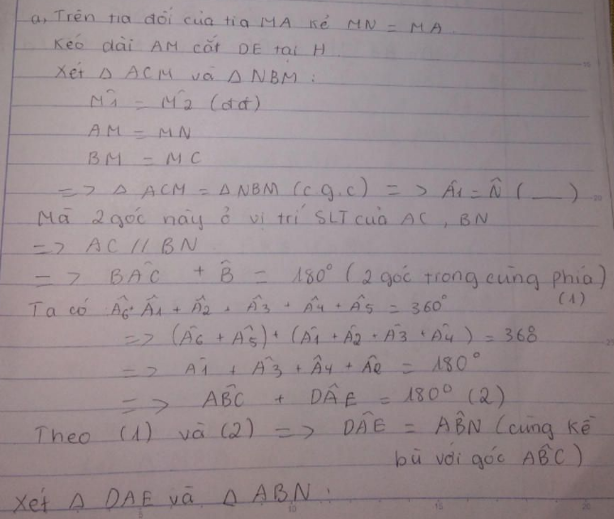
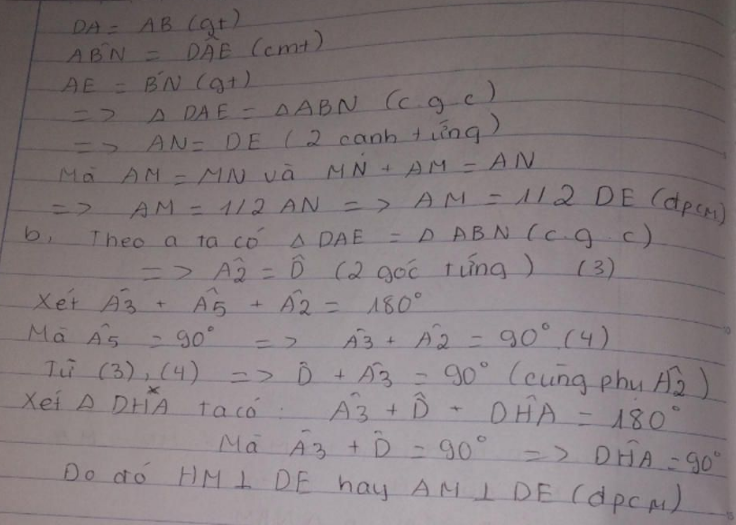

a:\(\widehat{DAC}=\widehat{DAB}+\widehat{BAC}=90^0+\widehat{BAC}\)
\(\widehat{BAE}=\widehat{BAC}+\widehat{CAE}=90^0+\widehat{BAC}\)
Do đó: \(\widehat{DAC}=\widehat{BAE}\)
Xét ΔDACvà ΔBAE có
AD=AB
\(\widehat{DAC}=\widehat{BAE}\)
AC=AE
Do đó: ΔDAC=ΔBAE
=>DC=BE
b: ΔDAC=ΔBAE
=>\(\widehat{ADC}=\widehat{ABE};\widehat{ACD}=\widehat{AEB}\)
\(\widehat{CEB}+\widehat{ECD}\)
\(=\widehat{CEB}+\widehat{ECA}+\widehat{DCA}\)
\(=\widehat{ECA}+\widehat{AEB}+\widehat{CEB}\)
\(=\widehat{ECA}+\widehat{AEC}=90^0\)
=>BE\(\perp\)CD