C1 Bác An mỗi tháng gửi tiết kiệm 10 000.000 đồng với suất 0,8%/năm. Hỏi sau 9 năm bác ấy đó nhận được tổng số tiền cả vốn và lãi là bao nhiêu? C2:Cho hình chóp S.ABCD đáy ABCD là hình bình hành tâm O; M là 1 điểm nằm trong tam giác SBC. Tìm giao tuyến của các cặp mp sau 1) Mp(SAC) và mp(SBD) 2) Mp(SAM) và mp(SBD).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án C
Gọi a là số tháng gửi với lãi suất 0,75% tháng, x là số tháng gửi với lãi suất 0,8%/tháng, khi đó số tháng gửi tiết kiệm là
![]()
Số tiền cả vốn lẫn lãi là
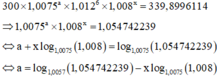
Thử 1 số giá trị của x:
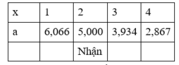
Vậy bác Minh gửi tiết kiệm trong thời gian 5 + 6 + 2 = 13 tháng.

Số tiền lúc đầu bác Khoa gửi là:
159750000*100/106,5=150000000(đồng)

Gọi số tiền bác An gửi là x
Sau 1 tháng bác An có được x*1,072(đồng)
Sau 2 tháng bác An có được x*1,072*1,072=x*1,072^2(đồng)
Theo đề, ta có:
x*1,072^2=151805400
=>x=132098428,1(đồng)

Giải thích các bước giải:
1% của 50 000 000 là:
50 000 000 : 100 = 500 000(đồng)
7 % của 50 000 000 là:
500 000 x 7 = 3 500 000(đồng)
Sau 1 năm tất cả tiền lãi và tiên gửi của bác An là:
50 000 000 + 3 500 000= 53 500 000(đồng)
Đáp số: 53 500 000 đồng.
HT~~~(^^)






Câu 2:
1: \(O\in AC\subset\left(SAC\right);O\in BD\subset\left(SBD\right)\)
=>\(O\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên \(\left(SAC\right)\cap\left(SBD\right)=SO\)
2:
Trong mp(SBC), gọi K là giao điểm của SM với BC
=>\(AK\subset\left(SAM\right)\)
Trong mp(ABCD), gọi E là giao điểm của BD và AK
\(E\in BD\subset\left(SBD\right);E\in AK\subset\left(SAM\right)\)
=>\(E\in\left(SAM\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAM\right)\cap\left(SBD\right)\)
nên \(\left(SAM\right)\cap\left(SBD\right)=SE\)
1:
Sau 9 năm bác đó nhận được số tiền là;
\(10\cdot10^6\cdot\left(1+0,8\%\right)^9=10743475,28\left(đồng\right)\)