Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Xét ΔCBD có M,N lần lượt là trung điểm của CD,CB
=>MN là đường trung bình của ΔCBD
=>MN//BD
mà \(BD\subset\left(ABD\right)\) và MN không nằm trong mp(ABD)
nên MN//(ABD)
b: Chọn mp(ACD) có chứa AM
\(CD\subset\left(ACD\right);CD\subset\left(BCD\right)\)
Do đó: \(\left(ACD\right)\cap\left(BCD\right)=CD\)
Ta có: \(M=AM\cap CD\)
=>M là giao điểm của AM với mp(BCD)
=>AM cắt mp(BCD) tại M
c: \(N\in BC\subset\left(ABC\right);A\in\left(ABC\right)\)
Do đó: \(AN\subset\left(ABC\right)\)
a: Xét ΔSBD có
H,K lần lượt là trung điểm của SB,SD
=>HK là đường trung bình của ΔSBD
=>HK//BD
mà \(BD\subset\left(ABCD\right)\);HK không thuộc (ABCD)
nên HK//(ABCD)
b: Chọn mp(SBD) có chứa BK
\(O\in BD\subset\left(SBD\right);O\in AC\subset\left(SAC\right)\)
=>\(O\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên \(\left(SAC\right)\cap\left(SBD\right)=SO\)
Gọi E là giao điểm của SO với BK
=>E là giao điểm của BK với mp(SAC)
=>BK cắt (SAC) tại E
c: \(O\in BD\subset\left(SBD\right);S\in\left(SBD\right)\)
Do đó: \(SO\subset\left(SBD\right)\)
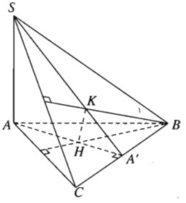
a) Gọi A’ là giao điểm của AH và BC. Ta cần chứng minh ba điểm S, K, A’ thẳng hàng.
Vì H là trực tâm của tam giác ABC nên AA′ ⊥ BC. Mặt khác theo giả thiết ta có: SA ⊥ (ABC), do đó SA ⊥ BC.
Từ đó ta suy ra BC ⊥ (SAA′) và BC ⊥ SA′. Vậy SA’ là đường cao của tam giác SBC nên SA’ là phải đi qua trực tâm K. Vậy ba đường thẳng AH, SK và BC đồng quy.
b) Vì K là trực tâm của tam giác SBC nên BK ⊥ SC (1)
Mặt khác ta có BH ⊥ AC vì H là trực tâm của tam giác ABC và BH ⊥ SA vì SA ⊥ (ABC).
Do đó BH ⊥ (ABC) nên BH ⊥ SC (2).
Từ (1) và (2) ta suy ra SC ⊥ (BHK). Vì mặt phẳng (SAC) chứa SC mà SC ⊥ (BHK) nên ta có (SAC) ⊥ (BHK).
c) Ta có
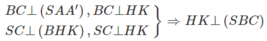
Mặt phẳng (BHK) chứa HK mà HK ⊥ (SBC) nên (BHK) ⊥ (SBC).
a: Xét ΔSAC có M,N lần lượt là trung điểm của SA,SC
=>MN là đường trung bình của ΔSAC
=>MN//AC
mà MN không thuộc mp(ABCD) và \(AC\subset\left(ABCD\right)\)
nên MN//(ABCD)
b: \(A\in AN;A\in\left(ABD\right)\)
=>\(A\in AN\cap\left(ABD\right)\)
mà \(N\in SC\) không thuộc mp(ABD)
nên \(A=AN\cap\left(ABD\right)\)
c: \(S\in\left(SAC\right);E\in AC\subset\left(SAC\right)\)
Do đó: \(SE\subset\left(SAC\right)\)
a: \(K\in HK;K\in BC\)
Do đó: HK cắt BC tại K
b: Xét ΔBAC có
H,K lần lượt là trung điểm của BA,BC
=>HK là đường trung bình
=>HK//AC
c: C thuộc BK
C thuộc CD
Do đó: BK cắt CD tại C
e: Trong mp(ABCD), ta có: HK và CD không song song vối nhau
=>HK cắt CD tại M
b: \(BD\subset\left(ABD\right)\)
=>BD nằm trong mp(ABD)
c: \(D\in CD\)
\(D\in\left(ABD\right)\)
Do đó: \(D=CD\cap\left(ABD\right)\)
=>CD cắt (ABD)
d: Xét ΔCBD có H,K lần lượt là trung điểm của CB,CD
=>HK là đường trung bình
=>HK//BD
=>HK//(ABD)
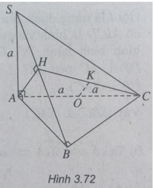
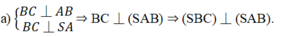
b) AH ⊥ SB mà SB là giao tuyến của hai mặt phẳng vuông góc là (SBC) và (SAB) nên AH ⊥ (SBC).
c) Xét tam giác vuông SAB với đường cao AH ta có:
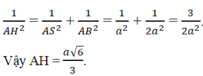
d) Vì OK ⊥ (SBC) mà AH ⊥ (SBC) nên OK // AH, ta có K thuộc CH.
OK = AH/2 = (a√6)/6.
a: Xét ΔSBC có SH/SB=SK/SC=1/2
nên HK//BC
mà \(BC\subset\left(ABC\right)\); HK không nằm trong mp(ABC)
nên HK//(ABC)
b: \(K\in SC\subset\left(SBC\right);K\in AK\)
Do đó: \(K\in AK\cap\left(SBC\right)\)
mà \(A\notin\left(SBC\right)\)
nên \(K=AK\cap\left(SBC\right)\)
c: \(A\in\left(SAB\right);H\in SB\subset\left(SAB\right)\)
Do đó: \(AH\subset\left(SAB\right)\)