Cho tam giác ABC hai đường phân giác của góc B và góc C cắt nhau tại O qua O kẻ đường thẳng song song với BC đường thẳng này cắt cạnh AB và AC lần lượt ở M và N a , tứ giácBCOM , BCNO là các hình gì b, Chứng minh MN = MP+ NC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 1 2021
a) Ta có: EF//BC(gt) =>\(\left\{{}\begin{matrix}\text{^EOB = ^OBC (SLT)}\\\text{ ^FOC = ^OCB (SLT)}\\\text{^AEF = ^B (Đồng vị)}\\\text{^AFE = ^C (Đồng vị)}\end{matrix}\right.\)
Có: ^OBC = ^OBA ( BF là phân giác ^B)
mà: ^EOB = ^OBC (cmt)
=> ^EOB = ^OBA => tam giác EBO cân tại E
Có: ^OCA = ^OCB ( BF là phân giác ^B)
mà: ^FOC = ^OCB (cmt)
=> ^FOC = ^OCA => tam giác FCO cân tại E
Ta có: ^AEF = ^B (cmt)
^AFE = ^C (cmt)
Mà ^B = ^C (tam giác ABC cân tại A)
=> ^AEF = ^AFE => tam giác AEF cân tại A
Có : ^ABF = ^CBF = \(\dfrac{1}{2}\) ^B ( BF là phân giác ^B)
^ACE = ^BCE = \(\dfrac{1}{2}\) ^B ( CF là phân giác ^C)
mà : ^B = ^C (tam giác ABC cân tại A)
=> ^ACE = ^ABF = ^CBF = ^BCE
Xét tg OBC có: ^OBC = ^OCB (^CBF = ^BCE) => tg OBC cân tại O
Xét tam giác FCO và tam giác EBO có:
^FOC = ^FOB ( đối đỉnh)
^FCO = ^EBO (^ABF = ^ACE)
OB = OC ( tg OBC cân tại O )
=> tam giác FCO = tam giác EBO(g-c-g)
15 tháng 3 2021
a) Xét tứ giác AEDF có
FD//AE(gt)
ED//AF(gt)
Do đó: AEDF là hình bình hành(Dấu hiệu nhận biết hình bình hành)
Hình bình hành AEDF có AD là tia phân giác của \(\widehat{FAE}\)(gt)
nên AEDF là hình thoi(Dấu hiệu nhận biết hình thoi)
KV
16 tháng 12 2023
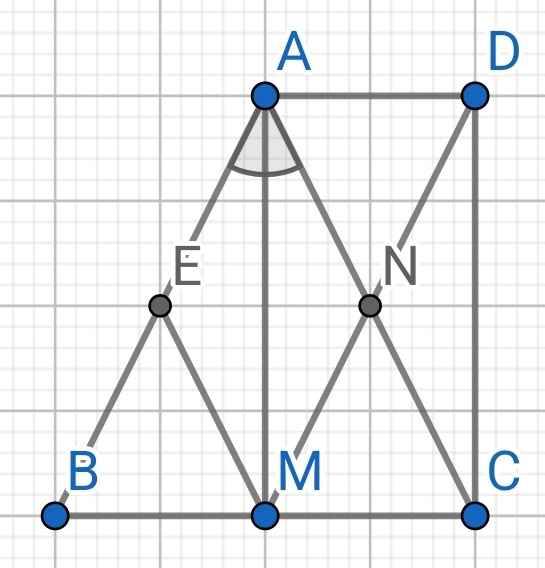a) Do MN // AB (gt)
⇒ MN // AE
Do ME // AC (gt)
⇒ ME // AN
Do AM là tia phân giác của ∠BAC (gt)
⇒ AM là tia phân giác của ∠EAN
Xét tứ giác AEMN có:
MN // AE (cmt)
ME // AN (cmt)
⇒ AEMN là hình bình hành
Mà AM là tia phân giác của ∠EAN (cmt)
⇒ AEMN là hình thoi
b) Do D là điểm đối xứng của M qua N (gt)
⇒ N là trung điểm của DM
∆ABC cân tại A có AM là tia phân giác của ∠BAC (gt)
⇒ AM cũng là đường trung trực của ∆ABC
⇒ M là trung điểm của BC
∆ABC có:
M là trung điểm của BC (cmt)
MN // AB (gt)
⇒ N là trung điểm của AC
Tứ giác ADCM có:
N là trung điểm của DM (cmt)
N là trung điểm của AC (cmt)
⇒ ADCM là hình bình hành
⇒ AD // CM
⇒ AD // BM
Do MN // AB (gt)
⇒ MD // AB
Tứ giác ADMB có:
MD // AB (cmt)
AD // BM (cmt)
⇒ ADMB là hình bình hành
1 tháng 10 2021
b: Xét ΔDBI có
\(\widehat{DBI}=\widehat{DIB}\)
nên ΔDBI cân tại D
Xét ΔEIC có \(\widehat{EIC}=\widehat{ECI}\)
nên ΔEIC cân tại E
Ta có: DE=DI+IE
nên DE=DB+EC
Vậy: BDEC là hình thang có một cạnh đáy bằng tổng hai cạnh bên
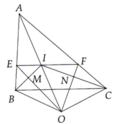
a: Xét tứ giác BCOM có MO//BC
nên BCOM là hình thang
Xét tứ giác BCNO có NO//BC
nên BCNO là hình thang
b: MO//BC
=>\(\widehat{MOB}=\widehat{OBC}\)
=>\(\widehat{MOB}=\widehat{MBO}\)
=>MO=MB
NO//BC
=>\(\widehat{NOC}=\widehat{OCB}\)
=>\(\widehat{NOC}=\widehat{NCO}\)
=>NO=NC
MN=MO+NO
=>MN=MB+NC