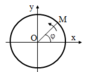
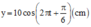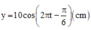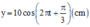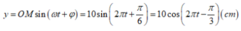Chất điểm M chuyển động trên đường tròn bán kính R = 2m với phương trình: s = 3t2 + t(hệ SI). Trong đó s là độ dài cung OM, O là điểm mốc trên đường tròn. Tính thời gian để chất điểm đi hết một vòng đầu tiên (lấy π = 3,14).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án C
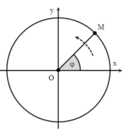
y = O M sin ( ω t + φ ) = 10 sin 2 π t + π 6 = 10 cos 2 π t − π 3 ( c m )

Đáp án D
+ Phương trình dao động của hình chiếu M lên Oy: y = 10 cos 2 πt − π 3

a, Ta có : \(T=\dfrac{1}{f}=\dfrac{1}{5}=0,2\left(s\right)\)
b, Ta có : \(C=2\pi r=0,3\pi\left(m\right)\)
\(\Rightarrow v=\dfrac{5C}{1}=\dfrac{5.0,3\pi}{1}=1,5\pi\left(m/s\right)\)
c,Ta có : \(\omega=\dfrac{2\pi}{T}=10\pi\left(rad/s\right)\)

Chọn A.
Góc quét được sau thời gian t: φ = ω t ⇒ φ M = 10 π t φ N = 5 π t
Hai chất điểm gặp nhau khi hiệu góc quét bằng một số nguyên lần 2 π tức là: k 2 π = φ M - φ N = 5 π t ⇒ t = 0 , 4 k ( s ) ( k = 1 ; 2 ; . . . )
Gặp nhau lần 3 ứng với k = 3 => t1 = 1,2(s)