Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a.
\(P=cos120^0+cos120^0+cos120^0=-\dfrac{3}{2}\)
b.
\(A=\dfrac{\dfrac{sinx}{cosx}-\dfrac{cosx}{cosx}}{\dfrac{sinx}{cosx}+\dfrac{cosx}{cosx}}=\dfrac{tanx-1}{tanx+1}=\dfrac{2-1}{2+1}=\dfrac{1}{3}\)
c.
\(A=\dfrac{cos\left(720+30\right)+sin\left(360+60\right)}{sin\left(-360+30\right)-cos\left(-360-30\right)}=\dfrac{cos30+sin60}{sin30-cos30}=-3-\sqrt{3}\)
Vì AH=(BC.1/2)tan60 ct lương giác
=BC.tan60.1/2=\(\sqrt{3}\)/2
họk tốt!
Do tam giác ABC vuông tại A và \(\widehat{B}=30^o\) \(\Rightarrow C=60^o\)
\(\Rightarrow\left(\overrightarrow{AB},\overrightarrow{BC}\right)=150^o;\)\(\left(\overrightarrow{BA},\overrightarrow{BC}\right)=30^o;\left(\overrightarrow{AC},\overrightarrow{CB}\right)=120^o\)
\(\left(\overrightarrow{AB},\overrightarrow{AC}\right)=90^o;\left(\overrightarrow{BC},\overrightarrow{BA}\right)=30^o\).Do vậy:
a) \(\cos\left(\overrightarrow{AB},\overrightarrow{BC}\right)+\sin\left(\overrightarrow{BA},\overrightarrow{BC}\right)+\tan\frac{\left(\overrightarrow{AC},\overrightarrow{CB}\right)}{2}\)
\(=\cos150^o+\sin30^o+\tan60^o\)
\(=-\frac{\sqrt{3}}{2}+\frac{1}{2}+\sqrt{3}\)
\(=\frac{\sqrt{3}+1}{2}\)
b) \(\sin\left(\overrightarrow{AB},\overrightarrow{AC}\right)+\cos\left(\overrightarrow{BC},\overrightarrow{AB}\right)+\cos\left(\overrightarrow{CA},\overrightarrow{BA}\right)\)
\(=\sin90^o+\cos30^o+\cos0^o\)
\(=1+\frac{\sqrt{3}}{2}\)
\(=\frac{2+\sqrt{3}}{2}\)
+) \(\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \widehat {ABC} = 60^\circ \)
+) Dựng hình bình hành ABCD, ta có: \(\overrightarrow {AD} = \overrightarrow {BC} \)
\( \Rightarrow \left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right) = \left( {\overrightarrow {AB} ,\overrightarrow {AD} } \right) = \widehat {BAD} = 120^\circ \)
+), Ta có: ABC là tam giác đều, H là trung điểm BC nên \(AH \bot BC\)
\(\left( {\overrightarrow {AH} ,\overrightarrow {BC} } \right) = \left( {\overrightarrow {AH} ,\overrightarrow {AD} } \right) = \widehat {HAD} = 90^\circ \)
+) Hai vectơ \(\overrightarrow {BH} \) và \(\overrightarrow {BC} \)cùng hướng nên \(\left( {\overrightarrow {BH} ,\overrightarrow {BC} } \right) = 0^\circ \)
+) Hai vectơ \(\overrightarrow {HB} \) và \(\overrightarrow {BC} \)ngược hướng nên \(\left( {\overrightarrow {HB} ,\overrightarrow {BC} } \right) = 180^\circ \)
Ta có I CA+AB I = I CB I =CB
Xét tam giác ABC ( A=90 ) áp dụng định lý pytago có
CB^2 = AB^2 + AC^2 = 9+16=25 => CB=5.
Vậy I CA+AB I= I CB I =5
Bạn lưu ý lần sau gõ lời giải bằng công thức toán (biểu tượng \(\sum\) góc trái khung soạn thảo) để được tick dễ dàng hơn khi làm đúng nhé.
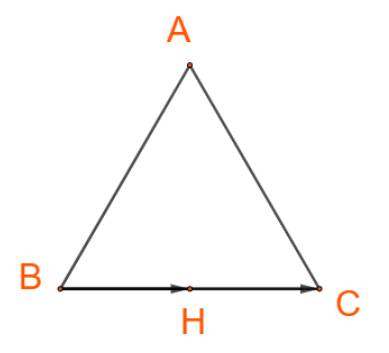
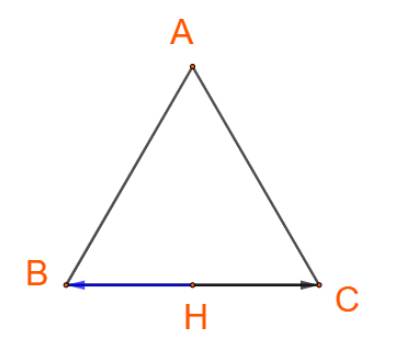
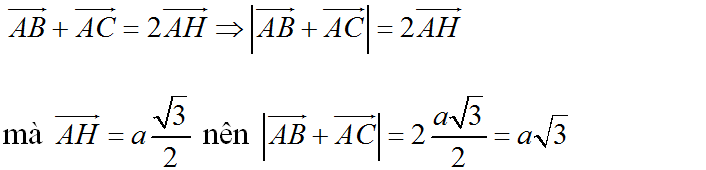
Gọi M là trung điểm của BC
Ta có: ΔABC đều
mà AM là đường trung tuyến
nên AM\(\perp\)BC tại M
Xét ΔAMB vuông tại M có \(sinB=\dfrac{AM}{AB}\)
=>\(\dfrac{AM}{1}=sin60=\dfrac{\sqrt{3}}{2}\)
=>\(AM=\dfrac{\sqrt{3}}{2}\)
Xét ΔABC có AM là đường trung tuyến
nên \(\overrightarrow{AB}+\overrightarrow{AC}=2\cdot\overrightarrow{AM}\)
=>\(\overrightarrow{AB}-\overrightarrow{CA}=2\cdot\overrightarrow{AM}\)
=>\(\left|\overrightarrow{AB}-\overrightarrow{CA}\right|=2\cdot AM=2\cdot\dfrac{\sqrt{3}}{2}=\sqrt{3}\)
=>A đúng, B và C đều sai
\(\left|\overrightarrow{AB}-\overrightarrow{AC}\right|\)
\(=\left|\overrightarrow{AB}+\overrightarrow{CA}\right|=\left|\overrightarrow{CB}\right|=CB=1\)
=>D sai