Dự báo thời tiết trong ba ngày thứ Hai, thứ Ba, thứ Tư của tuần sau cho biết, trong mỗi ngày này, khả năng có mưa và không mưa như nhau.
a) Vẽ sơ đồ hình cây mô tả không gian mẫu.
b) Tính xác suất của các biến cố:
F: “Trong ba ngày, có đúng một ngày có mưa”
G: “Trong ba ngày, có ít nhất hai ngày không mưa”.

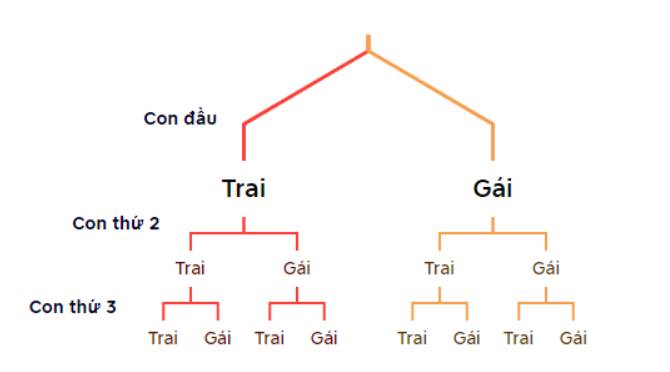
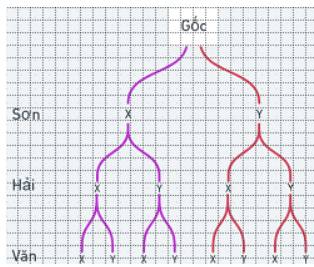

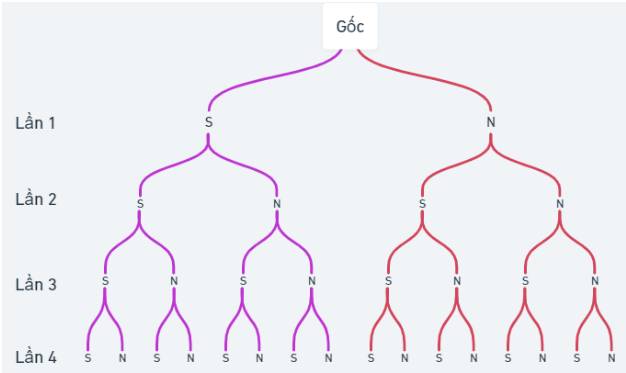
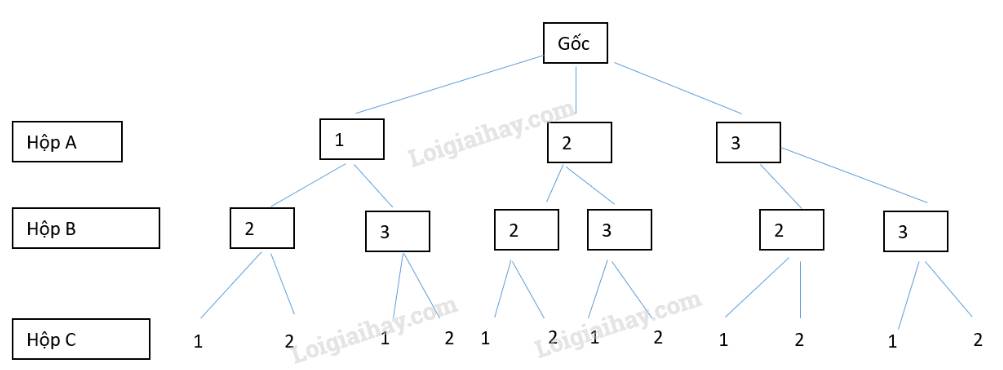
a) Sơ đồ cây trong đó B là ngày có mưa và A là nhà không mưa.
Dựa vào sơ đồ cây ta thấy \(n\left( \Omega \right) = 8\).
b) Ta có \(F = \left\{ {AAB,ABA,BAA} \right\}\). Vậy \(P\left( F \right) = \frac{3}{8}\).
\(G = \left\{ {AAB,ABA,BAA,AAA} \right\}\). Vậy \(P\left( G \right) = \frac{1}{2}\).