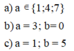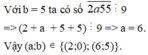Tìm tất cả các chữ số a và b để số \(\frac{ }{a459b}\) chia cho 2;5 và 9 đều dư 1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NH
1
28 tháng 10 2015
a459b chia cho 2;5;9 dư 1 => a459b -1 chia hết cho 2;5;9
+) a459b -1 chia hết cho 2;5 => a459b -1 có tận cùng là 0 => b = 1
=> a459b -1 = a4590 chia hết cho 9 => a+ 4 + 5 + 9 + 0 chia hết cho 9
=> a + 18 chia hết cho 9; 18 chia hết cho 9 nên a chia hết cho 9 => a = 9
Vậy a= 9; b = 0
TT
2
26 tháng 12 2015
Tìm tất cả các chữ số a và b để số a459b : 2 , 5, 9 đều dư 1
chia hết cho 2 và 5 dư 1 như vậy b = 1,
chia 9 dư 1 thì tổng: a+4+5+9+1 = 19+a là 1 số chia hết cho 9 dư 1 với điều kiện 0<a<10
như vậy a thỏa mãn là: a = 9
Vậy a = 9, b = 1 số cần tìm là 94591
NT
0
NH
1
11 tháng 5 2022
Cho A = a459b. Hãy thay a,b bằng những số thích hợp để a chia cho 2 , cho 5 , cho 9 đều có số dư là 1.
Cho B = 5x1y. Hãy thay x,y bằng những số thích hợp để được một số có 4 chữ số khác nhau chia cho 2, chia cho 3, chia cho 5 và số dư là 4.
Một số nhân với 9 thì được kết quả là 30862a3. Tìm số đó.
CM
27 tháng 3 2019
n chia hết cho 4 thì 8b phải chia hết cho 4. Vậy b = 0, 4 hoặc 8
n có 5 chữ số khác nhau nên b = 0 hoặc 4
Thay b = 0 thì n = a3780
+ Số a3780 chia hết cho 3 thì a = 3, 6 hoặc 9
+ Số n có 5 chữ số khác nhau nên a = 6 hoặc 9
Ta được các số 63 780 và 930780 thoả mãn điều kiện của đề bài
Thay b = 4 thì n = a3784
+ Số a3784 chia hết cho 3 thì a = 2, 5 hoặc 8
+ Số n có 5 chữ số khác nhau nên a = 2 hoặc 5. Ta được các số 23784 và 53 784 thoả mãn điều kiện đề bài
Các số phải tìm 63 780; 93 780; 23 784; 53 784.