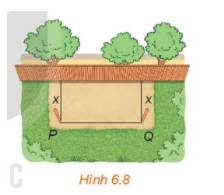
Xét bài toán rào vườn ở tình huống mở đầu. Gọi x mét \((0 < x < 10)\)là khoảng cách từ điểm cắm cọc đến bờ tường (H.6.8). Hãy tính theo x:
a) Độ dài cạnh PQ của mảnh đất.
b) Diện tích S(x) của mảnh đất được rào chắn.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giả sử điểm \(M\) có hoành độ là \(x\).
Độ dài \(OH\) là hoành độ của điểm \(M\). Vậy \(OH = x\).
Độ dài \(OK\) là tung độ của điểm \(M\). Vậy \(OK = \frac{1}{{{x^2}}}\).
\(S\left( x \right) = OH.OK = x.\frac{1}{{{x^2}}} = \frac{1}{x}\).
\(\mathop {\lim }\limits_{x \to {0^ + }} S\left( x \right) = \mathop {\lim }\limits_{x \to {0^ + }} \frac{1}{x} = + \infty \). Vậy diện tích \(S\left( x \right)\) trở nên rất lớn khi \(x \to {0^ + }\).
\(\mathop {\lim }\limits_{x \to + \infty } S\left( x \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{x} = 0\). Vậy diện tích \(S\left( x \right)\) dần về 0 khi \(x \to + \infty \).

a) Chiều rộng khu vườn hình chữ nhật là :
126 : 3 = 42 (m)
Chu vi khu vườn hình chữ nhật là :
(126 + 42) x 2 = 336 (m)
b) Độ dài đoạn cần rào dây théo gai là :
126 + 42 + 42 = 210 (m)
Số cọc bê tông cần chôn là :
210 : 2 + 1 = 106 (cọc)
Đáp số : 336m ; 106 cọc.

Qua 50 cái cọc sẽ có 49 khoảng, mỗi khoảng 1 m và 1 cái cổng 3m. Vậy:
Chu vi hình chữ nhật là: 49+3=52 m
Tổng chiều dài và rộng là: 52:2=26m
Chiều dài là: (26+6):2=16 m
Chiều rộng là: 26-16=10m
Diện tích mảnh vườn là: 16.10=160 m2

Để diện tích của mảnh vườn không nhỏ hơn 48 \({m^2}\)thì
\(S(x) \ge 48 \Rightarrow - 2{x^2} + 20x \ge 48 \Leftrightarrow - 2{x^2} + 20x - 48 \ge 0\)

a) Chiều rộng khu vườn hình chữ nhật là :
126 : 3 = 42 (m)
Chu vi khu vườn hình chữ nhật là :
(126 + 42) x 2 = 336 (m)
b) Độ dài đoạn cần rào dây théo gai là :
126 + 42 + 42 = 210 (m)
Số cọc bê tông cần chôn là :
210 : 2 + 1 = 106 (cọc)
Đáp số : 336m ; 106 cọc.

Giải
a)Diện tích mảnh đất hình chữ nhật là:
20.6=120(mét vuông)
b)Diện tích vườn hoa hình thoi là:
120-80=40(mét vuông)
Độ dài đường chéo thứ nhất là:
40.2:8=10(m)
Đáp số:a) 120 mét vuông b)10 m
a) Theo bài ra ta có: \(x + x + PQ = 20 \Rightarrow PQ = 20 - 2x\)(m)
b) Diện tích của mảnh đất được rào chắn là: \(\)\(x.PQ = x.(20 - 2x) = - 2{x^2} + 20x({m^2})\)