4x2+2ax+a-1 ======phân tích đa thức thành nhân tử đó bạn làm giúm mik nha
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 10 2021
\(1,\\ a,=4\left(x-2\right)^2+y\left(x-2\right)=\left(4x-8+y\right)\left(x-2\right)\\ b,=3a^2\left(x-y\right)+ab\left(x-y\right)=a\left(3a+b\right)\left(x-y\right)\\ 2,\\ a,=\left(x-y\right)\left[x\left(x-y\right)^2-y-y^2\right]\\ =\left(x-y\right)\left(x^3-2x^2y+xy^2-y-y^2\right)\\ b,=2ax^2\left(x+3\right)+6a\left(x+3\right)\\ =2a\left(x^2+3\right)\left(x+3\right)\\ 3,\\ a,=xy\left(x-y\right)-3\left(x-y\right)=\left(xy-3\right)\left(x-y\right)\\ b,Sửa:3ax^2+3bx^2+ax+bx+5a+5b\\ =3x^2\left(a+b\right)+x\left(a+b\right)+5\left(a+b\right)\\ =\left(3x^2+x+5\right)\left(a+b\right)\\ 4,\\ A=\left(b+3\right)\left(a-b\right)\\ A=\left(1997+3\right)\left(2003-1997\right)=2000\cdot6=12000\\ 5,\\ a,\Leftrightarrow\left(x-2017\right)\left(8x-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2017\\x=\dfrac{1}{4}\end{matrix}\right.\\ b,\Leftrightarrow\left(x-1\right)\left(x^2-16\right)=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=4\\x=-4\end{matrix}\right.\)
14 tháng 8 2021
a: \(4x^2-x-5=\left(4x-5\right)\left(x+1\right)\)
b: \(x^2-2x-15=\left(x-5\right)\left(x+3\right)\)
9 tháng 10 2021
\(ax^2+a-axy+2ax-ay\)
\(a\left(x^2+2x+1\right)-ay\left(x+1\right)\)
\(a\left(x+1\right)^2-ay\left(x+1\right)\)
\(\left(x+1\right)\left[a\left(x+1\right)-ay\right]\)
\(\left(x+1\right)\left(ax+a-ay\right)\)
\(a\left(x+1\right)\left(x+1-y\right)\)
GH
2
TM
12 tháng 12 2021
a/ \(4x^2-9\)
\(=\left(2x-3\right)\left(2x+3\right)\)
b/ \(3x\left(3x-2\right)+1\)
\(=9x^2-6x+1\)
\(=\left(3x-1\right)^2\)
12 tháng 12 2021
\(a,=\left(2x-3\right)\left(2x+3\right)\)
\(b,=9x^2-6x+1=\left(3x-1\right)^2\)
T
11 tháng 12 2023
a) $4x^2+4x+1$
$=(2x)^2+2\cdot2x\cdot1+1^2$
$=(2x+1)^2$
b) $x^2+6x-y^2+9$
$=(x^2+6x+9)-y^2$
$=(x^2+2\cdot x\cdot3+3^2)-y^2$
$=(x+3)^2-y^2$
$=(x+3-y)(x+3+y)$
$\text{#}Toru$
11 tháng 12 2023
a: \(4x^2+4x+1\)
\(=\left(2x\right)^2+2\cdot2x\cdot1+1^2\)
\(=\left(2x+1\right)^2\)
b: \(x^2+6x-y^2+9\)
\(=\left(x^2+6x+9\right)-y^2\)
\(=\left(x+3\right)^2-y^2\)
\(=\left(x+3+y\right)\left(x+3-y\right)\)
LD
1
8 tháng 11 2021
a: \(=x\left(x^2+4x+4-z^2\right)\)
\(=x\left(x+2-z\right)\left(x+2+z\right)\)
AH
Akai Haruma
Giáo viên
31 tháng 7 2021
Lời giải:
a. Không phân tích được thành nhân tử
b. \(a^4+a^2-22=(a^2+\frac{1}{2})^2-\frac{89}{4}=(a^2+\frac{1-\sqrt{89}}{2})(a^2+\frac{1+\sqrt{89}}{2})\)
(thông thường nhân tử là số hữu tỉ, phân tích kiểu này như cố để thành nhân tử cũng không hợp lý lắm, bạn coi lại đề)
c.
$x^4+4x^2-5=(x^4-x^2)+(5x^2-5)$
$=x^2(x^2-1)+5(x^2-1)=(x^2-1)(x^2+5)=(x-1)(x+1)(x^2+5)$
NV
1
AH
Akai Haruma
Giáo viên
19 tháng 8 2023
Lời giải:
$x^2-y^2+a^2-b^2+2ax+2by=(x^2+a^2+2ax)-(y^2+b^2-2by)$
$=(x+a)^2-(y-b)^2=(x+a-y+b)(x+a+y-b)$
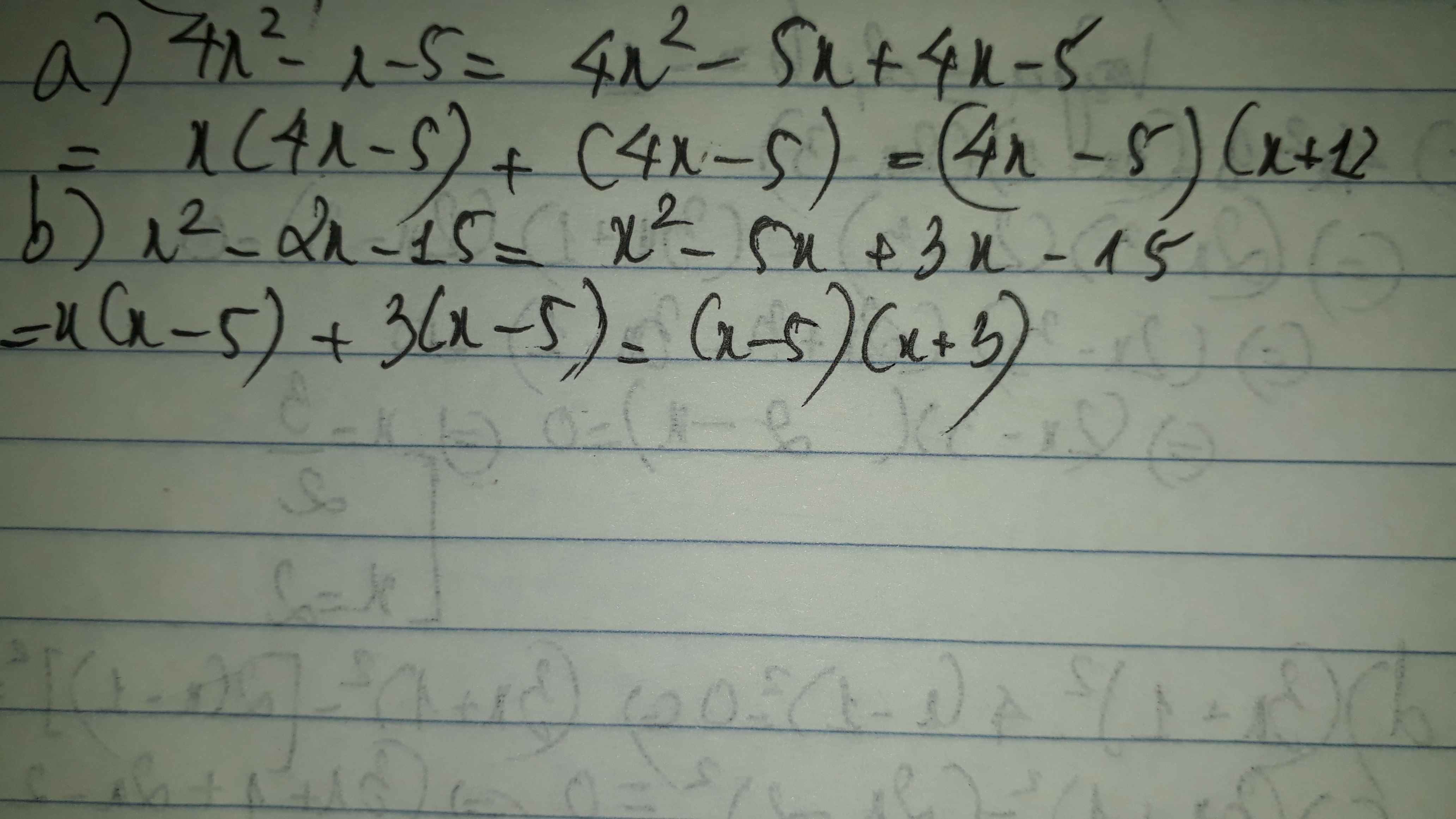
\(4x^2+2ax+a-1=\left(4x^2-1\right)+\left(2ax+a\right)=\left(2x+1\right).\left(2x-1\right)+a.\left(2x+1\right)\)
\(=\left(2x+1\right).\left(2x-1+a\right)\)
\(4x^2+2ax+a-1\)
= \(\left[\left(2x\right)^2-1\right]+a\left(2x+1\right)\)
= \(\left(2x-1\right)\left(2x+1\right)+a\left(2x+1\right)\)
=\(\left(2x+1\right)\left(2x-1+a\right)\)