Trong mặt phẳng, cho 6 đường thẳng song song và 8 đường thẳng song song cùng vuông góc với 6 đường thẳng đó. Có bao nhiêu hình chữ nhật được tạo thành?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Việc lập một hình chữ nhật được thực hiện bởi hai bước:
+ Chọn 2 đường thẳng trong số 4 đường thẳng.
Có: 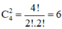 cách chọn.
cách chọn.
+ Chọn 2 đường thẳng trong số 5 đường thẳng vuông góc
Có: 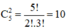 cách chọn.
cách chọn.
⇒ Theo quy tắc nhân: Có 10.6 = 60 (cách lập hình chữ nhật).

Cứ hai đường thẳng trong 4 đường thẳng hợp với 2 đường trong 5 đường thẳng vuông góc với chúng tạo thành một hình chữ nhật.
Có C42 = 6 cách chọn 2 đường thẳng trong 4 đường thẳng song song thứ nhất.
Có C52 = 10 cách chọn 2 đường thẳng trong 5 đường thẳng vuông góc với các đường thẳng trên.
Vậy số hình chữ nhật được tạo thành là: 6.10 = 60 cách
Trong mặt phẳng có bao nhiêu hình chữ nhật được tạo thành từ bốn đường thẳng song song với nhau và năm đường thẳng vuông góc với bốn đường thằng song song đó ?
Bài giải:
Để lập được một hình chữ nhât, phải thực hiện liên tiếp hai hành động sau đây:
Hành động 1: Chọn đường thẳng (không phân biệt thứ tự) từ nhóm đường thẳng song song đã cho. Số các cách để thực hiện hành động này là (cách)
Hành động 2: Chọn đường thẳng (không phân biệt thứ tự) từ nhóm đường thẳng đã cho, vuông góc với đường thẳng song song. Số các cách để thực hiện hành động này là
(cách).
Theo quy tắc nhân suy ra số các cách để lập thành một hình chữ nhật từ các đường thẳng đã cho là (cách).
Qua trên suy ra từ các đường thẳng đã cho có thể lập được hình chữ nhât.

Để lập được một hình chữ nhât, phải thực hiện liên tiếp hai hành động sau đây:
Hành động 1: Chọn 2 đường thẳng (không phân biệt thứ tự) từ nhóm 4 đường thẳng song song đã cho. Số các cách để thực hiện hành động này là C24 = = 6 (cách)
Hành động 2: Chọn 2 đường thẳng (không phân biệt thứ tự) từ nhóm 5 đường thẳng đã cho, vuông góc với 4 đường thẳng song song. Số các cách để thực hiện hành động này là
C25 = = 10 (cách).
Theo quy tắc nhân suy ra số các cách để lập thành một hình chữ nhật từ các đường thẳng đã cho là 6 . 10 = 60 (cách).
Qua trên suy ra từ các đường thẳng đã cho có thể lập được 60 hình chữ nhât.

Đáp án A.
Dễ thấy m và n càng chênh lệch ít thì số hình chữ nhật được tạo ra càng nhiều. Do đó số hình chữ nhật được tạo ra là lớn nhất nếu m = 7 ; n = 8 hoặc ngược lại. Để cho dễ hình dung ta xét trường hợp có 7 đường nằm ngang và 8 đường thẳng đứng. Cứ hai đường nằm ngang kết hợp với hai đường thẳng đứng thì tạo thành một hình chữ nhật. Vậy số hình chữ nhật là C 7 2 × C 8 2 = 588 .

Đáp án A.
Dễ thấy m và n càng chênh lệch ít thì số hình chữ nhật được tạo ra càng nhiều. Do đó số hình chữ nhật được tạo ra là lớn nhất nếu m = 7 , n = 8 hoặc ngược lại. Để cho dễ hình dung ta xét trường hợp có 7 đường nằm ngang và 8 đường thẳng đứng. Cứ hai đường nằm ngang kết hợp với hai đường thẳng đứng thì tạo thành một hình chữ nhật. Vậy số hình chữ nhật là C 7 2 × C 7 2 = 588 .

Đáp án C
2. Nếu 3 mặt phẳng đôi một cắt nhau theo 3 giao tuyến phân biệt thì 3 giao tuyến ấy hoặc đồng quy, hoặc đôi một song song với nhau
8. Cho 2 đường thẳng chéo nhau. Có duy nhất một mặt phẳng chứa đường thẳng này và song song với đường thẳng kia

Có 144 góc vuông
Ta có : 2 đường thẳng song song nằm ngang và 2 đường thẳng song song nằm dọc tạo thành 4 x 4 = 16 góc vuông
=> Mỗi một giao điểm có 4 góc vuông
mà có 36 giao điểm
=> 36 x 4 = 144 góc vuông.
ko bíc giải thích vầy có đúng khum (sai thì cho mk xin lỗi:<)
Số cách chọn 2 đường thằng song song trong 6 đường thằng song song là: \(C_6^2\) (cách chọn)
Số cách chọn 2 đường thằng song song trong 8 đường thằng song song cùng vuông góc với 6 đường thằng song song ban đầu là: \(C_8^2\) (cách chọn)
Áp dụng quy tắc nhân, ta có số hình chữ nhật có thể tạo thành là: \(C_8^2.C_6^2 = 420\) ( hình chữ nhật)