a) Có bao nhiêu cách xếp 20 học sinh theo một hàng dọc?
A.\({20^{20}}\) B.\(20!\) C. 20 D.1
b) Số cách chọn ra 3 học sinh từ một lớp có 40 học sinh là:
A. \(A_{40}^3\) B. \({40^3}\) C. \({3^{40}}\) D.\(C_{40}^3\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do yêu cầu xếp xen kẽ nên chỉ có thể xếp theo phương án: người đầu tiên là nam, sau đó xen kẽ nam, nữ và người xếp cuối cùng cũng sẽ là nam.
Số cách xếp 20 bạn nam thành một hàng là 20!. Khi đó giữa các bạn nam có 19 khoảng trống để xếp 19 bạn nữ, có 19! cách xếp các bạn nữ.
Theo quy tắc nhân ta được số cách xếp thỏa mãn là 20!.19!.
Chọn C.

Số học sinh tham gia đồng diễn thể dục là:
15×24=360 (học sinh)
Số hàng ngang xếp được là:
360:20=18 (hàng)
Đáp số: 18 hàng.
Đáp án C

Xếp 3 hàng, không thừa, không thiếu bạn nào; vậy số học sinh chia hết cho 3.
Xếp 5 hàng, không thừa không thiếu bạn nào; vậy số học sinh chia hết cho 5.
Số vừa chia hết cho 3 vừa chia hết cho 5 là : 0; 15; 30; 45; …
Mà lớp ít hơn 35 học sinh nhiều hơn 20 học sinh nên có 30 học sinh.

Xếp 3 hàng, không thừa, không thiếu bạn nào; vậy số học sinh chia hết cho 3.
Xếp 5 hàng, không thừa không thiếu bạn nào; vậy số học sinh chia hết cho 5.
Số vừa chia hết cho 3 vừa chia hết cho 5 là : 0; 15; 30; 45; …
Mà lớp ít hơn 35 học sinh nhiều hơn 20 học sinh nên có 30 học sinh.

Bài làm
Số học sinh của lớp đó phải chia hết cho 3 và 5 .
Chia cho 3 gồm các số : 21 ; 24 ; 27 ; 30 .
Chia cho 5 gồm các số : 25 ; 30 .
=> Số đó là : 30 .
Vậy lớp học đó có 30 học sinh .
Mình cũng không chắc nữa , bạn kham thảo thử !
Gọi số HS là a (20<a<35)
Ta có: a vừa chia hết cho 3, vừa chia hết cho 5 nên a phải lần lượt bằng 15;30;45;60;...
mà 20<a<35 nên a= 30
Vậy có tất cả 30 HS

Đáp án D
Số phần tử không gian mẫu là: C 40 4 = 91390 .
Số cách chọn 4 học sinh có cả học sinh xếp loại giỏi, khá, trung bình là:
C 10 2 . C 20 1 . C 10 1 + C 10 1 . C 20 2 . C 10 1 + C 10 1 . C 20 1 . C 10 2 = 37000
Số cách chọn 4 học sinh nam có cả học sinh xếp loại giỏi, khá, trung bình là:
C 5 2 . C 9 1 . C 6 1 + C 5 1 . C 9 2 . C 6 1 + C 5 1 . C 9 1 . C 6 2 = 2295
Số cách chọn 4 học sinh nữ có cả học sinh xếp loại giỏi, khá, trung bình là:
C 5 2 . C 11 1 . C 4 1 + C 5 1 . C 11 2 . C 4 1 + C 5 1 . C 11 1 . C 4 2 = 1870
Số cách chọn 4 học sinh có cả nam, nữ có cả học sinh xếp loại giỏi, khá, trung bình là:
37000 - 2295 - 1870 = 32835
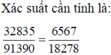


Số cách chọn 4 học sinh có cả học sinh xếp loại giỏi, khá, trung bình là:
![]()
Số cách chọn 4 học sinh nam có cả học sinh xếp loại giỏi, khá, trung bình là:
![]()
Số cách chọn 4 học sinh nữ có cả học sinh xếp loại giỏi, khá, trung bình là:
![]()
Số cách chọn 4 học sinh có cả nam, nữ có cả học sinh xếp loại giỏi, khá, trung bình là:
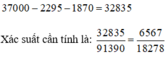
Chọn D
a) Số cách xếp 20 học sinh theo một hàng dọc là: \(20!\) (cách xếp). Vậy ta chọn đáp án B.
b) Số cách chọn ra 3 học sinh từ một lớp có 40 học sinh là: \(C_{40}^3\) (cách chọn). Vậy ta chọn đáp án D.