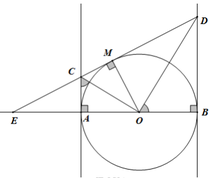
Cho nửa đường tròn (O) đường kính AB= 2R. Gọi (d) là tiếp tuyến của (O) tại B. Trên cùng AB lấy điểm M tuỳ ý (M không trùng với A và B), tía AM cắt (d) tại điểm N. Gọi C là trung điểm của AM, tia CO cắt (d) tại điểm D
1. Chứng minh OBNC là tứ giác nội tiếp.
2. Chứng minh: ON ⊥ AD và CA. CN = CO. CD
3. Xác định vị trí điểm M trên cung AB để tổng AN +2AM đạt giá trị nhỏ nhất.