Cho hình vuông ABCD có tâm I (Hình 1).
a) Tính \(\widehat {IDC}\).
b) Tìm hai vectơ cùng có điểm đầu là D và điểm cuối lần lượt là I và C
c) Tìm hai vectơ có điểm đầu là D và lần lượt bằng vectơ \(\overrightarrow {IB} \)và \(\overrightarrow {AB} \)

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do M và N lần lượt là trung điểm của BC và AC nên MN là đường trung bình của tam giác AB.

Đáp án B

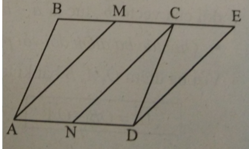
Do ABCD là hình bình hành nên: AD = BC.
Lại có; M và N lần lượt là trung điểm của BC; AD nên : AN = ND= BM = MC.


Chắc là lục giác đều?
Các vecto bằng \(\overrightarrow{AB}\) là \(\overrightarrow{FO};\overrightarrow{OC};\overrightarrow{ED}\)

a) I là tâm của ABCD, suy ra \(\widehat {IDC} = 45^\circ \)
b) Vectơ có điểm đầu là D và điểm cuối là I là \(\overrightarrow {DI} \)
Vectơ có điểm đầu là D và điểm cuối là C là \(\overrightarrow {DC} \)
c) Vectơ có điểm đầu là D và bằng vectơ \(\overrightarrow {IB} \) là \(\overrightarrow {DI} \)
Vectơ có điểm đầu là D và bằng vectơ \(\overrightarrow {AB} \) là \(\overrightarrow {DC} \)