Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Khẳng định trên sai. Vì khi 3 điểm phân biệt A, B, C thẳng hàng thì hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) cùng phương nhưng chưa chắc là cùng hướng.
Chẳng hạn:
Khi A nằm giữa B và C thì hướng của vectơ \(\overrightarrow {AB} \) là từ phải sang trái, còn hướng của vectơ \(\overrightarrow {AC} \)là từ trái sang phải nên hai vectơ này là ngược hướng.
Do các vectơ đều nằm trên đường thẳng AB nên các vectơ này đều cùng phương với nhau.
Dễ thấy:
Các vectơ \(\overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {BC} \) cùng hướng (từ trái sang phải.)
Các vectơ \(\overrightarrow {BA} ,\overrightarrow {CA} ,\overrightarrow {CB} \) cùng hướng (từ phải sang trái.)
Do đó, các cặp vectơ cùng hướng là:
\(\overrightarrow {AB} \) và \(\overrightarrow {AC} \); \(\overrightarrow {AC} \) và \(\overrightarrow {BC} \); \(\overrightarrow {AB} \) và \(\overrightarrow {BC} \); \(\overrightarrow {BA} \) và \(\overrightarrow {CA} \); \(\overrightarrow {BA} \) và \(\overrightarrow {CB} \);\(\overrightarrow {BA} \) và \(\overrightarrow {CB} \).
Các cặp vectơ ngược hướng là:
\(\overrightarrow {AB} \) và \(\overrightarrow {BA} \); \(\overrightarrow {AB} \) và \(\overrightarrow {CA} \); \(\overrightarrow {AB} \) và \(\overrightarrow {CB} \);
\(\overrightarrow {AC} \) và \(\overrightarrow {BA} \); \(\overrightarrow {AC} \) và \(\overrightarrow {CA} \); \(\overrightarrow {AC} \) và \(\overrightarrow {CB} \);
\(\overrightarrow {BC} \) và \(\overrightarrow {BA} \); \(\overrightarrow {BC} \) và \(\overrightarrow {CA} \); \(\overrightarrow {BC} \) và \(\overrightarrow {CB} \);
a) Gọi M, N lần lượt là điểm đầu và điểm cuối của vecto \(\overrightarrow a \).
Vì \(\overrightarrow a = \overrightarrow {AB} \Leftrightarrow \overrightarrow {MN} = \overrightarrow {AB} \) nên tứ giác MNBA là hình bình hành.
Nói cách khác B là đỉnh thứ tư của hình bình hành tạo bởi vecto \(\overrightarrow a \) và điểm A.
Tương tự, C là đỉnh thứ tư của hình bình hành tạo bởi vecto \(\overrightarrow b \) và điểm B.
b) Dễ thấy: tổng của hai vecto \(\overrightarrow {AB} \) và \(\overrightarrow {BC} \) là vecto \(\overrightarrow {AC} \).
Do đó tổng của hai vecto \(\overrightarrow a \) và \(\overrightarrow b \)bằng vecto \(\overrightarrow {AC} \).
Ta có viết: \(\overrightarrow a + \overrightarrow b = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
a)\(\overrightarrow{AB}+\overrightarrow{AN}=\overrightarrow{AM}\)
b)\(\overrightarrow{BA}+\overrightarrow{CN}=2\overrightarrow{BA}\)
c)Có \(\overrightarrow{AB}=\overrightarrow{NC}\)=>bt trở thành \(\overrightarrow{NC}+MC+\overrightarrow{MN}=\overrightarrow{MC}-\overrightarrow{MC}=vt0\)
d)có vt BA+vt BC=vtBN
bt trở thành vtMN-vtMN=vt0
hok tốt!
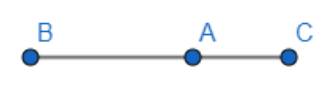
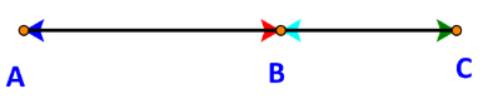
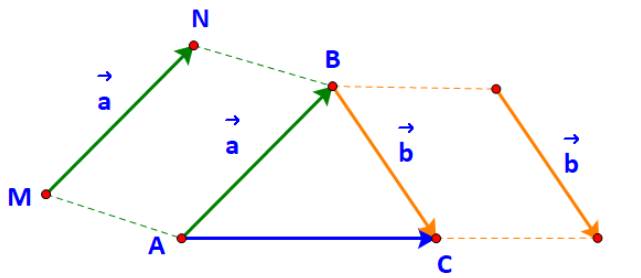
a) Nếu A, B, C thẳng hàng thì đường thẳng AB trùng đường thẳng AC, do đó hai vecto \(\overrightarrow {AB} ,\overrightarrow {AC} \) cùng phương.
b) Nếu hai vecto \(\overrightarrow {AB} ,\overrightarrow {AC} \) cùng phương thì đường thẳng AB trùng đường thẳng AC, do đó ba điểm A, B, C có thẳng hàng.