Cho đường tròn tâm O. Giả sử A, B là hai điểm nằm trên đường tròn. Tìm điều kiện cần và đủ để hai vecto \(\overrightarrow {OA} \) và \(\overrightarrow {OB} \) đối nhau.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NM
19 tháng 8 2017
Trước tiên ta chứng minh với A, B, C là ba góc của 1 tam giác thì:
\(cos\left(2A\right)+cos\left(2B\right)+cos\left(2C\right)>-1\)
Ta có:
\(cos^2A+cos^2B+cos^2C=\frac{1+cos\left(2A\right)}{2}+\frac{1+cos\left(2B\right)}{2}+cos^2C\)
\(=1+\frac{cos\left(2A\right)+cos\left(2B\right)}{2}+cos^2C\)
\(=1+cos\left(A+B\right).cos\left(A-B\right)+cos^2C\)
\(=1-cos\left(C\right).cos\left(A-B\right)+cos^2C\)
\(=1-cos\left(C\right)\left(cos\left(A-B\right)-cosC\right)\)
\(=1-cos\left(C\right)\left(cos\left(A-B\right)-cos\left(A+B\right)\right)\)
\(=1-2cos\left(A\right).cos\left(B\right).cos\left(C\right)\)
Ta lại có:
\(-1\le cosA\le1;-1\le cosB\le1;-1\le cosC\le1\)
\(\Rightarrow cosA.cosB.cosC< 1\)
\(\Rightarrow cos\left(2A\right)+cos\left(2B\right)+cos\left(2C\right)=1-2cosA.cosB.cosC>1-2=-1\)
Quay lại bài toán ta có:
TH 1: Trong \(\overrightarrow{OA};\overrightarrow{OB};\overrightarrow{OC}\) có 2 vecto cùng phương ngược chiều giả sử là \(\overrightarrow{OA};\overrightarrow{OB}\) thì
\(\Rightarrow|\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}|=|\overrightarrow{OC}|=OC=1\)
TH 2: Cả 3 vecto không cùng phương với nhau ta có ABC tạo thành tam giác.
\(|\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}|^2=OA^2+OB^2+OC^2+2\left(\overrightarrow{OA}.\overrightarrow{OB}+\overrightarrow{OB}.\overrightarrow{OC}+\overrightarrow{OC}.\overrightarrow{OA}\right)\)
\(=3+2\left(cos\left(2A\right)+cos\left(2B\right)+cos\left(2C\right)\right)>3-2=1\)
Đâu = xảy ra khi trong ba vecto có 2 vecto cùng phương ngược chiều. Hay khi khi tam giác ABC là tam giác vuông.
19 tháng 8 2017
Trước tiên ta chứng minh với A, B, C là ba góc của 1 tam giác thì:
cos(2A)+cos(2B)+cos(2C)>−1
Ta có:
cos2A+cos2B+cos2C=1+cos(2A)2 +1+cos(2B)2 +cos2C
=1+cos(2A)+cos(2B)2 +cos2C
=1+cos(A+B).cos(A−B)+cos2C
=1−cos(C).cos(A−B)+cos2C
=1−cos(C)(cos(A−B)−cosC)
=1−cos(C)(cos(A−B)−cos(A+B))
=1−2cos(A).cos(B).cos(C)
Ta lại có:
−1≤cosA≤1;−1≤cosB≤1;−1≤cosC≤1
⇒cosA.cosB.cosC<1
⇒cos(2A)+cos(2B)+cos(2C)=1−2cosA.cosB.cosC>1−2=−1
Quay lại bài toán ta có:
TH 1: Trong →OA;→OB;→OC có 2 vecto cùng phương ngược chiều giả sử là →OA;→OB thì
⇒|→OA+→OB+→OC|=|→OC|=OC=1
TH 2: Cả 3 vecto không cùng phương với nhau ta có ABC tạo thành tam giác.
|→OA+→OB+→OC|2=OA2+OB2+OC2+2(→OA.→OB+→OB.→OC+→OC.→OA)
=3+2(cos(2A)+cos(2B)+cos(2C))>3−2=1
Đâu = xảy ra khi trong ba vecto có 2 vecto cùng phương ngược chiều. Hay khi khi tam giác ABC là tam giác vuông.
24 tháng 9 2023
Tham khảo:
a) \(\overrightarrow {AB} \) và \(\overrightarrow {AM} \) ngược hướng
\( \Leftrightarrow \left\{ \begin{array}{l}AB//AM\\B \; \text {và}\; M \; \text {nằm cùng phía so với điểm A}\end{array} \right.\)
\( \Leftrightarrow \) A, B, thẳng hàng và A nằm giữa B và M
b) \(\overrightarrow {MA} \) và \(\overrightarrow {MB} \) cùng phương
TH1: \(MA < MB\)
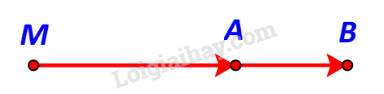
M, A, B thẳng hàng & A nằm giữa M và B.
TH2: \(MA > MB\)
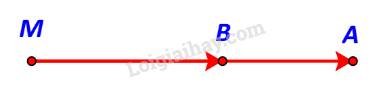
M, A, B thẳng hàng & B nằm giữa M và A.
c) \(\overrightarrow {AB} \) và \(\overrightarrow {AM} \) cùng hướng
TH1: \(AM < AB\)
A, M, B thẳng hàng & M nằm giữa A và B.
TH2: \(AB < AM\)
A, M, B thẳng hàng & B nằm giữa A và M.
d) \(\overrightarrow {MA} \) và \(\overrightarrow {MB} \) ngược hướng
\( \Leftrightarrow \left\{ \begin{array}{l}MA//MB\\A \; \text {và} \; B\; \text {nằm về hai phía so với điểm M}\end{array} \right.\)
\( \Leftrightarrow \) A, M, B thẳng hàng & M nằm giữa A và B.
Vậy điều kiện cần và đủ để M nằm giữa A và B là d) \(\overrightarrow {MA} \) và \(\overrightarrow {MB} \) ngược hướng
14 tháng 4 2016
Vì : \(\overrightarrow{MN}=\overrightarrow{OA}\Rightarrow T_{\overrightarrow{OA}}:M\rightarrow N\). Do đó N nằm trên đường tròn ảnh của (O;R) . Mặt khác N lại nằm trên (O’;R’) do đó N là giao của đường tròn ảnh với với (O’;R’) . Từ đó suy ra cách tìm :
- Vè đường tròn tâm A bán kính R , đường tròn náy cắt (O’;R’) tại N
- Kẻ đường thẳng d qua N và song song với OA , suy ra d cắt (O;R) tại M
| = |
|.cos(
, 
.
= 
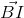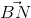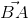lý luận tương tự.
)
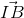Hai vecto \(\overrightarrow {OA} \) và \(\overrightarrow {OB} \) đối nhau \( \Leftrightarrow \) hai tia OA, OB đối nhau và OA = OB.
\( \Leftrightarrow \) O là trung điểm của AB hay AB là đường kính của đường tròn (O).
Vậy điều kiện cần và đủ để hai vecto \(\overrightarrow {OA} \) và \(\overrightarrow {OB} \) đối nhau là AB là đường kính của đường tròn (O).