Gọi \(\mathbb{R}\) là tập hợp các số thực, I là tập hợp các số vô tỉ. Khi đó \(I \subset \mathbb{R}\). Tìm tập hợp những số thực không phải là số vô tỉ.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(A = \{ x \in \mathbb{N}|\;x < 2\} = \{ 0;1\} \) và \(B = \{ x \in \mathbb{R}|\;{x^2} - x = 0\} = \{ 0;1\} \)
Vậy A = B, A là tập con của tập B và ngược lại.
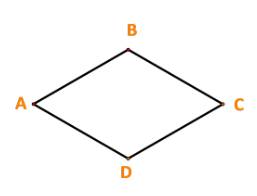
b) D là tập hợp con của C vì: Mỗi hình vuông đều là một hình thoi đặc biệt: hình thoi có một góc vuông.
\(C \ne D\) vì có nhiều hình thoi không là hình vuông, chẳng hạn:
c) \(E = ( - 1;1] = \left\{ {x \in \mathbb{R}|\; - 1 < x \le 1} \right\}\) và \(F = ( - \infty ;2] = \left\{ {x \in \mathbb{R}|\;x \le 2} \right\}\)
E là tập con của F vì \( - 1 < x \le 1 \Rightarrow x \le 2\) .
\(E \ne F\) vì \( - 3 \in F\)nhưng \( - 3 \notin E\)

a) A là tập hợp các số tự nhiên nhỏ hơn 5, khi đó \(0 \in A,2 \in A,3 \in A.\)
B là tập hợp các nghiệm thực của phương trình \({x^2} - 3x + 2 = 0\), khi đó \(1 \in B,2 \in B.\)
C là tập hợp các thứ trong tuần, khi đó chủ nhật \( \in C,\) thứ năm \( \in C.\)
b)
\(\begin{array}{l}0 \in \mathbb{N},\;2 \in \mathbb{N}, - 5 \notin \mathbb{N},\;\frac{2}{3} \notin \mathbb{N}.\\0 \in \mathbb{Z},\; - 5 \in \mathbb{Z},\frac{2}{3} \notin \mathbb{Z},\sqrt 2 \; \notin \mathbb{Z}.\\0 \in \mathbb{Q},\;\frac{2}{3} \in \mathbb{Q},\sqrt 2 \notin \mathbb{Q},\;\pi \notin \mathbb{Q}.\\\frac{2}{3} \in \mathbb{R},\;\sqrt 2 \in \mathbb{R},e \notin \mathbb{R},\;\pi \notin \mathbb{R}.\end{array}\)

a) Phép cộng và phép trừ
b) Phép trừ
c) Phép trừ, phép nhân và phép chia
a) Tập hợp các số hữu tỉ khác 0 tất cả các phép cộng, trừ, nhân , chia luôn thực hiện được
b) Tập hợp các số hữu tỉ dương : phép trừ không phải luôn thực hiện được
Ví dụ: (1/3) - (3/4) kết quả không phải là số hữu tỉ dương
c) Tập hợp các số hữu tỉ âm: phép trừ, nhân và chia không phải luôn luôn thực hiện được
Ví dụ: (-1/3) - (-3/4) kết quả không phải là số hữu tỉ âm

Các số \( - 1; - 2; - 3;...\) là các số nguyên âm.
Các số 0;1;2;3;... là các số tự nhiên.
\(\mathbb{Z}\) là tập hợp gồm các số tự nhiên và các số nguyên âm.

Ta có: \({x^2} - 6 = 0 \Leftrightarrow x = \pm \sqrt 6 \in \mathbb{R}\)
Vì \(\sqrt 6 \in \mathbb{R}\) và \( -\sqrt 6 \in \mathbb{R}\) nên \( A = \left\{ { \pm \sqrt 6 } \right\}\)
Nhưng \( \pm \sqrt 6 \notin \mathbb{Z}\) nên không tồn tại \(x \in \mathbb{Z}\) để \({x^2} - 6 = 0\)
Hay \(B = \emptyset \).
Tập hợp các số thực không phải là số vô tỉ chính là tập hợp \(\mathbb{Q}\) các số hữu tỉ.