Thời gian ra sân (giờ) của một số cựu cầu thủ ở giải ngoại hạng Anh qua các thời kì được cho như sau:
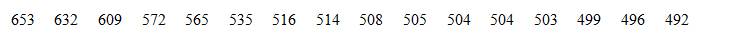
(Theo: https://www.premierleague.com/)
Hãy chuyển mẫu số liệu trên sang dạng ghép nhóm với bảy nhóm có độ dài bằng nhau
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Chuyển dữ liệu từ bảng số liệu ban đầu ở trên sang dạng bảng thống kê sau đây:
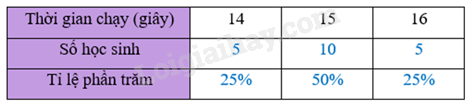
b) Biểu đồ cột biểu diễn thời gian chạy 100 m (tính theo giây) của 20 học sinh nam:
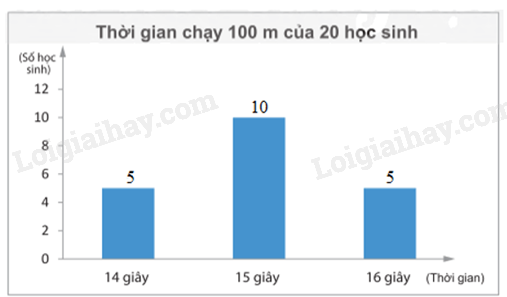
Biểu đồ hình quạt tròn biểu diễn thời gian chạy 100 m (tính theo giây) của 20 học sinh nam:
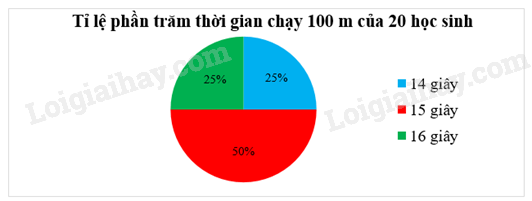

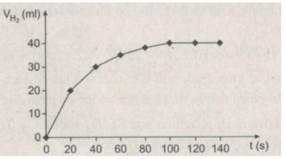
Từ 0 giây đến 20 giây là đoạn đồ thị dốc nhất, đó là khoảng thời gian phản ứng có tốc độ cao nhất.
Ở thời điểm phản ứng kết thúc, đồ thị nằm ngang, thể tích hiđro thu được là cực đại 40 ml. Tại thời điểm đó axit clohiđric đã phản ứng hết.

Dòng điện chuyển từ tăng sang giảm tại thời điểm : t = t2.
Và ngược lại dòng điện chuyển từ giảm sang tăng tại thời điểm : t = 0 và t = t4.
→ Đáp án D

a) Sắp xếp lại dãy số liệu theo thứ tự không giảm:

Tứ phân vị thứ nhất là: \(\frac{1}{2}\left( {{x_5} + {x_6}} \right) = \frac{1}{2}\left( {11 + 11} \right) = 11\)
Tứ phân vị thứ hai là: \(\frac{1}{2}\left( {{x_{10}} + {x_{11}}} \right) = \frac{1}{2}\left( {14 + 14} \right) = 14\)
Tứ phân vị thứ ba là: \(\frac{1}{2}\left( {{x_{15}} + {x_{16}}} \right) = \frac{1}{2}\left( {21 + 22} \right) = 21,5\)
b)

c) Do số trận đấu là số nguyên nên ta hiệu chỉnh như sau:

Tổng trận đấu là: \(n = 4 + 8 + 2 + 6 = 20\).
Gọi \({x_1};{x_2};...;{x_{20}}\) là điểm số của các trận đấu được xếp theo thứ tự không giảm.
Ta có:
\({x_1},...,{x_4} \in \begin{array}{*{20}{c}}{\left[ {5,5;10,5} \right)}\end{array};{x_5},...,{x_{12}} \in \begin{array}{*{20}{c}}{\left[ {10,5;15,5} \right)}\end{array};{x_{13}},{x_{14}} \in \begin{array}{*{20}{c}}{\left[ {15,5;20,5} \right)}\end{array};{x_{15}},...,{x_{20}} \in \begin{array}{*{20}{c}}{\left[ {20,5;25,5} \right)}\end{array}\)
• Tứ phân vị thứ hai của dãy số liệu là: \(\frac{1}{2}\left( {{x_{10}} + {x_{11}}} \right)\)
Ta có: \(n = 20;{n_m} = 8;C = 4;{u_m} = 10,5;{u_{m + 1}} = 15,5\)
Do \({x_{10}},{x_{11}} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\left[ {10,5;15,5} \right)}\end{array}}\end{array}\) nên tứ phân vị thứ hai của dãy số liệu là:
\({Q_2} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 10,5 + \frac{{\frac{{20}}{2} - 4}}{8}.\left( {15,5 - 10,5} \right) = 14,25\)
• Tứ phân vị thứ nhất của dãy số liệu là: \(\frac{1}{2}\left( {{x_5} + {x_6}} \right)\).
Ta có: \(n = 20;{n_m} = 8;C = 4;{u_m} = 10,5;{u_{m + 1}} = 15,5\)
Do \({x_5},{x_6} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\left[ {10,5;15,5} \right)}\end{array}}\end{array}\) nên tứ phân vị thứ nhất của dãy số liệu là:
\({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 10,5 + \frac{{\frac{{20}}{4} - 4}}{8}.\left( {15,5 - 10,5} \right) = 11,125\)
• Tứ phân vị thứ ba của dãy số liệu là: \(\frac{1}{2}\left( {{x_{15}} + {x_{16}}} \right)\).
Ta có: \(n = 20;{n_j} = 6;C = 4 + 8 + 2 = 14;{u_j} = 20,5;{u_{j + 1}} = 25,5\)
Do \({x_{15}},{x_{16}} \in \begin{array}{*{20}{c}}{\left[ {20,5;25,5} \right)}\end{array}\) nên tứ phân vị thứ ba của dãy số liệu là:
\({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right) = 20,5 + \frac{{\frac{{3.20}}{4} - 14}}{6}.\left( {25,5 - 20,5} \right) \approx 21,3\)

Đáp án B.
Từ đồ thị ta thấy: tại t = 0 vận tốc của tàu là v0 = 2 m/s2 và tàu đang chuyển động nhanh dần với gia tốc:
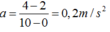
Áp dụng
![]()
![]()
Chú ý: Từ đồ thị cho ta biết và a từ đó ta có thể tính tiếp các đại lượng khác

Trong mẫu số liệu trên; các giá trị 15; 13; 16 đều xuất hiện nhiều nhất – là 3 lần.
Do đó; mốt của mẫu số liệu trên là : 15; 13; 16
Chọn D

gia su 11 cau thu la 11 diem
chon 1 diem noi voi 10 diem con lai ta duoc 10 duong thang
co tat ca 11 diem nen so duong thang la: 11.10 (duong thang)
nhung nhu vay moi duong thang duoc tinh hai lan, nen so duong thang thuc su co la: (11.10):2=55 (duong thang)
Tham khảo:
Giá trị lớn nhất là: 653.
Giá trị bé nhất là: 492.
Khoảng biến thiên là: 653 - 492 = 161.
Để chia thành 7 nhóm có độ dài bằng nhau, ta lấy điểm đầu mút trái của nhóm đầu tiên là 492, điểm đầu mút phải của nhóm cuối là 653 với độ dài mỗi nhóm là 23.
Ta có mẫu số liệu ghép nhóm sau: