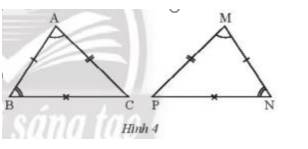
Quan sát Hình 4. Hai tam giác ABC và MNP có bằng nhau không? Hãy chỉ ra các cặp góc và các cặp cạnh tương ứng bằng nhau.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Các cặp cạnh tương ứng : FE = KH , ED = HG , DF = GK
Các góc tương ứng : góc F = góc K, góc E = góc H, góc D = góc G
Kí hiệu bằng nhau của tam giác đó : ΔDFE=ΔGKH
Ta có: Các cặp góc tương ứng là: \(\widehat E = \widehat H;\widehat D = \widehat G;\widehat F = \widehat K\)
Các cặp cạnh tương ứng là:\(ED=HG;EF=HK;DF=GK\)

a) AB = A’B’; BC = B’C’; CA = C’A’.
A = A’; B = B’; C = C’.
b) Hai tam giác ABC và A’B’C’ có bằng nhau vì chúng có các cặp cạnh và cặp góc tương ứng bằng nhau.
c) Hai hình tam giác ABC và A’B’C’ có thể đặt chồng khít lên nhau.

Vì \(\widehat A = \widehat E\), \(\widehat C = \widehat D\) nên đỉnh A tương ứng với đỉnh E, đỉnh C tương ứng với đỉnh D.
\( \Rightarrow \widehat B = \widehat F\) ( 2 góc tương ứng)
Do đó, \(\Delta{ABC}=\Delta{EFD}\)
\(\Rightarrow AB = DE;BC = EF;AC = DF\)( các cạnh tương ứng )

a)
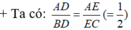
Nên theo định lí ta- let đảo ta có: DE // BC.
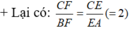
Nên theo định lí ta- let đảo ta có: EF // AB.
b) Tứ giác BDEF là hình bình hành vì có các cặp cạnh đối song song với nhau
c) Tứ giác BDEF là hình bình hành ⇒ DE = BF = 7
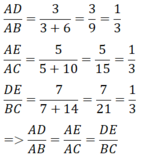
Ba cạnh của ΔADE tương ứng tỉ lệ với ba cạnh của ΔABC
\( \Rightarrow \Delta{ABC}=\Delta{MNP}\) do có các cặp góc và cạnh tương ứng bằng nhau.
Các cặp góc bằng nhau là: \(\widehat A = \widehat M\); \(\widehat B = \widehat N\);\(\widehat C = \widehat P\)
Các cặp cạnh bằng nhau là: \(AB = MN; AC = MP; BC = PN\)