Thực hiện phép chia.
a) \((45{x^5} - 5{x^4} + 10{x^2}):5{x^2}\)
b) \((9{t^2} - 3{t^4} + 27{t^5}):3t\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
QT
1
20 tháng 9 2023
Tham khảo:
a) \((4{x^2} - 5):(x - 2) = \dfrac{{4{x^2} - 5}}{{x - 2}} = 4x + 8 + \dfrac{{11}}{{x - 2}}\)
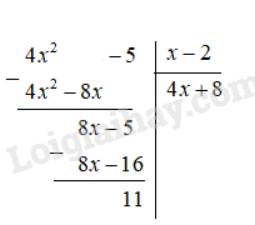
Vậy \( (4{x^2} - 5):(x - 2)= 4x + 8 + \dfrac{{11}}{{x - 2}}\)
b) \((3{x^3} - 7x + 2):(2{x^2} - 3) = \dfrac{{3{x^3} - 7x + 2}}{{2{x^2} - 3}}\)
Vậy \( (3{x^3} - 7x + 2):(2{x^2} - 3)= \dfrac{3}{2}x + \dfrac{{\dfrac{-5}{2}x + 2}}{{2{x^2} - 3}}\)
HQ
Hà Quang Minh
Giáo viên
20 tháng 9 2023
\(a)(2{y^4} - 13{y^3} + 15{y^2} + 11y - 3):({y^2} - 4y - 3)=2y^2-5y+1\)
b) \((5{x^3} - 3{x^2} + 10):({x^2} + 1)=5x-3+\dfrac{-5x+13}{x^2+1}\)
20 tháng 9 2023
Tham khảo:
a) \((8{x^6} - 4{x^5} + 12{x^4} - 20{x^3}):4{x^3}\)
\( = (8{x^6}:4{x^3}) - (4{x^5}:4{x^3}) + (12{x^4}:4{x^3}) - (20{x^3}:4{x^3})\)
\( = 2{x^2} - {x^2} + 3x - 5\)
b)
Vậy \((2{x^2} - 5x + 3):(2x - 3)= x - 1\)
HQ
Hà Quang Minh
Giáo viên
9 tháng 9 2023
\(\begin{array}{l}a)\frac{{4{\rm{x}} - 6}}{{5{{\rm{x}}^2} - x}}.\frac{{25{{\rm{x}}^2} - 10{\rm{x}} + 1}}{{27 + 8{{\rm{x}}^3}}}\\ = \frac{{ - 2\left( {3 - 2{\rm{x}}} \right)}}{{x\left( {5{\rm{x}} - 1} \right)}}.\frac{{{{\left( {5{\rm{x}} - 1} \right)}^2}}}{{\left( {3 - 2{\rm{x}}} \right)\left( {9 + 6{\rm{x}} + 4{{\rm{x}}^2}} \right)}}\\ = \frac{{ - 2\left( {5{\rm{x}} - 1} \right)}}{{x\left( {9 + 6{\rm{x}} + 4{{\rm{x}}^2}} \right)}}\\b)\frac{{2{\rm{x}} + 10}}{{{{\left( {x - 3} \right)}^2}}}:\frac{{{{\left( {x + 5} \right)}^3}}}{{{x^2} - 9}}\\ = \frac{{2{\rm{x}} + 10}}{{{{\left( {x - 3} \right)}^2}}}.\frac{{{x^2} - 9}}{{{{\left( {x + 5} \right)}^2}}}\\ = \frac{{2\left( {x + 5} \right)\left( {x - 3} \right)\left( {x + 3} \right)}}{{{{\left( {x - 3} \right)}^2}{{\left( {x + 5} \right)}^3}}}\\ = \frac{{2\left( {x + 3} \right)}}{{\left( {x - 3} \right){{\left( {x + 5} \right)}^2}}}\end{array}\)
NT
2
26 tháng 12 2021
\(a.\dfrac{3^{27}}{9^6.3^{16}}=\dfrac{3^{27}}{3^{12}.3^{16}}=\dfrac{3^{27}}{3^{28}}=\dfrac{1}{3}\)
\(\left(x-\dfrac{5}{2}\right)^2=\dfrac{9}{4}\\ \Rightarrow x-\dfrac{5}{2}=\pm\dfrac{3}{2}\)
\(TH1:x-\dfrac{5}{2}=\dfrac{3}{2}\Rightarrow x=\dfrac{3}{2}+\dfrac{5}{2}=\dfrac{8}{2}=4\)
\(TH2:x-\dfrac{5}{2}=-\dfrac{3}{2}\Rightarrow x=-\dfrac{3}{2}+\dfrac{5}{2}=\dfrac{2}{2}=1\)
26 tháng 12 2021
a: \(=\dfrac{3^{27}}{3^{12}\cdot3^{16}}=\dfrac{1}{3}\)
20 tháng 10 2017
Bài 1: Thực hiện phép tính:
a) 50 . 79 + 24 : 23 - 15
= 1 . 79 + 24 : 8 - 15
= 79 + 3 - 15
= 82 - 15
= 67.
b) 27 . 34 + 34 . 73
= (27 + 73) . 34
= 100 . 34
= 3400.
c) 43 . 46 + 54 . 43 - 120
= 43. (46 + 54) - 120
= 64 . 100 - 120
= 6400 - 120
= 6280.
d) 2 + 3 + 4 + ... + 69 + 70
= (70 + 2) . [(70 - 2) : 1 + 1] : 2
= 72 . 69 : 2
= 4968 : 2
= 2484.
Bài 2: Tìm số tự nhiên x, biết:
a) 5x = 25
\(\Rightarrow\) 5x = 52
\(\Rightarrow\) x = 2.
b) 3x + 2 = 81
3x . 32 = 81
\(\Rightarrow\) 3x . 32 = 34
\(\Rightarrow\) x + 2 = 4
x = 4 - 2
x = 2.
c) (x + 1)3 = 27
\(\Rightarrow\) (x + 1)3 = 33
\(\Rightarrow\) x + 1 = 3
x = 3 - 1
x = 2.
d) 6 : (2x - 1) + 45 = 490 . 47
6 : (2x - 1) + 45 = 1 . 47
6 : (2x - 1) + 45 = 47
6 : (2x - 1) = 47 - 45
6 : (2x - 1) = 2
2x - 1 = 6 : 2
2x - 1 = 3
2x = 3 + 1
2x = 4
x = 4 : 2
x = 2.
Bài 3: Tính:
a) 27 . 75 + 25 . 27 - 100
= 27 . (75 + 25) - 100
= 27 . 100 - 100
= 2700 - 100
= 2600.
b) 47 : 45 - 35 : 5 + 27 : 32
= 42 - 7 + 27 : 9
= 16 - 7 + 3
= 9 + 3
= 12.
c) 210 : 27 + 40030 . 29 - 135 : 45
= 23 + 1 . 29 - 135 : 45
= 8 + 29 - 3
= 37 - 3
= 34.
d) 12 : {390 : [500 - (125 + 35 . 7)]}
= 12 : {390 : [500 - (125 + 245)]
= 12 : {390 : [500 - 370]}
= 12 : {390 : 130}
= 12 : 3
= 4.
G
19 tháng 9 2017
Giải:
Bài 1:
\(707-3\left(x+3\right)=407\)
\(\Leftrightarrow3\left(x-3\right)=300\)
\(\Leftrightarrow x+3=100\)
\(\Leftrightarrow x=97\)
Vậy \(x=97\).
Bài 2:
a) \(143-43.\left[\left(25:5\right)^2-5^2\right]\)
\(=143-43.\left(5^2-5^2\right)\)
\(=143-43.1\)
\(=143-43=100\)
b) \(7:7+49\left(2^3.15-5.4\right)\)
\(=1+49.\left(120-20\right)\)
\(=1+49.100\)
\(=4901\)
c) \(\left(2^3.9^4+9^3.45\right):\left(9^2.10-9^2\right)\)
\(=\left(8.9^4+9^4.5\right):\left(9^2.10-9^2\right)\)
\(=\left[9^4\left(8+5\right)\right]:\left[9^2\left(10-1\right)\right]\)
\(=9^4.13:9^3\)
\(=9.13=117\)
Chúc bạn học tốt!
7 tháng 7 2023
a: =16-2+91=14+91=105
b: =9*5+8*10-27=45+53=98
c: =32+65-3*8=8+65=73
d; \(=5^3-10^2=125-100=25\)
e: \(=4^2-3^2+1=8\)
f: =9*16-16*8-8+16*4
=16(9-8+4)-8
=16*5-8
=72
H9
HT.Phong (9A5)
CTVHS
7 tháng 7 2023
a) \(2^4-50:25+13\cdot7\)
\(=2^4-2+91\)
\(=16-2+91\)
\(=14+91\)
\(=105\)
b) \(3^2\cdot5+2^3\cdot10-3^4:3\)
\(=9\cdot5+8\cdot10-3^3\)
\(=45+80-27\)
\(=98\)
c) \(2^5+5\cdot13-3\cdot2^3\)
\(=32+65-3\cdot8\)
\(=32+65-24\)
\(=73\)
d) \(5^{13}:5^{10}-5^2\cdot2^2\)
\(=5^{13-10}-\left(5\cdot2\right)^2\)
\(=5^3-10^2\)
\(=125-100\)
\(=25\)
e) \(4^5:4^3-3^9:3^7+5^0\)
\(=4^{5-3}-3^{9-7}+1\)
\(=4^2-3^2+1\)
\(=16-9+1\)
\(=8\)
f) \(3^2\cdot2^4-2^3\cdot4^2-2^3\cdot5^0+4^2\cdot2^2\)
\(=3^2\cdot4^2-2^3\cdot4^2-2^3\cdot1+4^2\cdot2^2\)
\(=4^2\cdot\left(3^2-2^3+2^2\right)-2^3\)
\(=4^2\cdot\left(9-8+4\right)-8\)
\(=16\cdot5-8\)
\(=72\)
Tham khảo:
a) \((45{x^5} - 5{x^4} + 10{x^2}):5{x^2}\)\( = 9{x^3} - {x^2} + 2\)
b) \((9{t^2} - 3{t^4} + 27{t^5}):3t = (27{t^5} - 3{t^4} + 9{t^2}):3t\\=(27t^5):(3t) - (3t^4):(3t)+(9t^2):(3t) = 9{t^4} - {t^3}+3t\)