Giúp mình câu b,c,d;cần gấp trong hôm nay ! Cảm ơn trước ạ !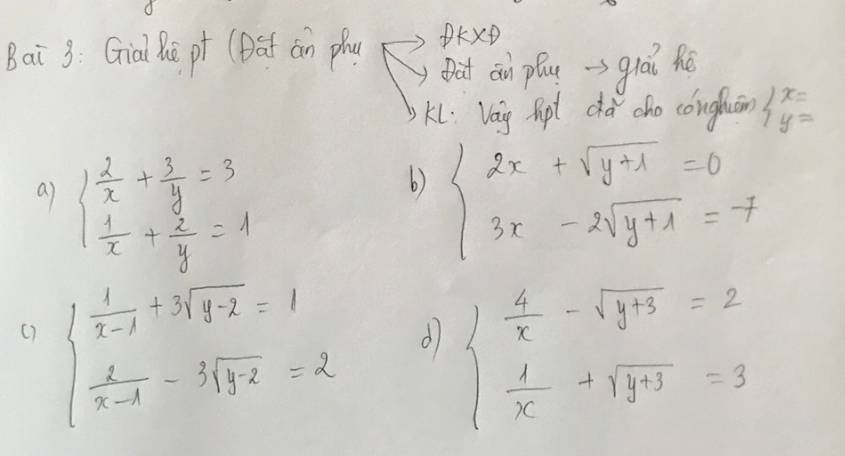
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
AH
1
Những câu hỏi liên quan
23 tháng 10 2021
\(b,N=\left(2x-1\right)^2-4\ge-4\\ N_{min}=-4\Leftrightarrow x=\dfrac{1}{2}\\ c,P=\left(2x-5\right)^2+6\left(2x-5\right)+9-4\\ P=\left(2x-5+3\right)^2-4=\left(2x-2\right)^2-4\ge-4\\ P_{min}=-4\Leftrightarrow x=1\\ d,Q=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1\\ Q=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\\ Q_{min}=1\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
AH
Akai Haruma
Giáo viên
23 tháng 10 2021
6a.
$M=x^2-x+1=(x^2-x+\frac{1}{4})+\frac{3}{4}$
$=(x-\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}$
Vậy $M_{\min}=\frac{3}{4}$ khi $x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}$
NT
3 tháng 9 2021
b. Ta có ∠GHE=360°-(90°+70°+60°)=140°
mà ∠GHE+x=180°⇒x=180°-140°=40°
c. Ta có 2x=360°-(65°+95°)=200°⇒x=200°:2=100°
d. Ta có ∠LKJ=180°-120°=60°
⇒x=360°-(95°+120°+60°)=85°
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 3 2023
a.
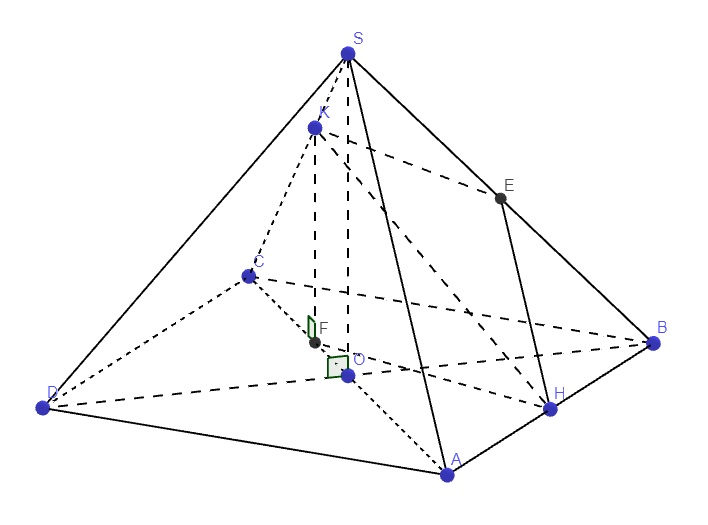
\(O=AC\cap BD\Rightarrow O\in BD\in\left(SBD\right)\) \(\Rightarrow SO\in\left(SBD\right)\)
\(\left\{{}\begin{matrix}SO\perp\left(ABCD\right)\Rightarrow SO\perp AC\\AC\perp BD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow AC\perp\left(SBD\right)\Rightarrow AC\perp SD\)
b.
O là trung điểm AC, H là trung điểm AB \(\Rightarrow\) OH là đường trung bình tam giác ABC
\(\Rightarrow OH||BC\Rightarrow OH\perp AB\Rightarrow OH\perp CD\) (1)
Mà \(SO\perp\left(ABCD\right)\Rightarrow SO\perp CD\) (2)
(1);(2) \(\Rightarrow CD\perp\left(SHO\right)\)
c.
Theo cmt trên \(OH||BC\Rightarrow OH||AD\)
\(\Rightarrow\widehat{\left(OH;SD\right)}=\widehat{\left(AD;SD\right)}=\widehat{SDA}\)
\(AC=2a\sqrt{2}\Rightarrow OA=a\sqrt{2}\Rightarrow SA=SB=SC=SD=\sqrt{SO^2+OA^2}=a\sqrt{3}\)
Áp dụng định lý hàm cosin trong tam giác SAD:
\(cos\widehat{SDA}=\dfrac{SD^2+AD^2-SA^2}{2SD.AD}=\dfrac{\sqrt{3}}{3}\)
\(\Rightarrow\widehat{SDA}=...\)
24 tháng 11 2023
a: \(x^3y+x-y-1\)
\(=\left(x^3y-y\right)+\left(x-1\right)\)
\(=y\left(x^3-1\right)+\left(x-1\right)\)
\(=y\left(x-1\right)\left(x^2+x+1\right)+\left(x-1\right)\)
\(=\left(x-1\right)\left(x^2y+xy+y+1\right)\)
b: \(x^2\left(x-2\right)+4\left(2-x\right)\)
\(=x^2\left(x-2\right)-4\left(x-2\right)\)
\(=\left(x-2\right)\left(x^2-4\right)\)
\(=\left(x-2\right)\cdot\left(x-2\right)\left(x+2\right)=\left(x+2\right)\cdot\left(x-2\right)^2\)
c: \(x^3-x^2-20x\)
\(=x\cdot x^2-x\cdot x-x\cdot20\)
\(=x\left(x^2-x-20\right)\)
\(=x\left(x^2-5x+4x-20\right)\)
\(=x\left[x\left(x-5\right)+4\left(x-5\right)\right]\)
\(=x\left(x-5\right)\left(x+4\right)\)
d: \(\left(x^2+1\right)^2-\left(x+1\right)^2\)
\(=\left(x^2+1+x+1\right)\left(x^2+1-x-1\right)\)
\(=\left(x^2+x+2\right)\left(x^2-x\right)\)
\(=x\left(x-1\right)\left(x^2+x+2\right)\)
mình xin lỗi vì ảnh kia bị lỗi. Giúp mình câu a,b,c,d nha còn biểu đồ mình đã làm câu 1.4 và 2.4 r nên mn giúp mình các câu còn lại nhé. Cám ơn
VQ
1
b: ĐKXĐ: y>=-1
Đặt \(\left\{{}\begin{matrix}x=a\\\sqrt{y+1}=b\left(b>=0\right)\end{matrix}\right.\)
Hệ phương trình sẽ trở thành:
2a+b=0 và 3a-2b=-7
=>4a+2b=0 và 3a-2b=-7
=>a=-1 và b=2
=>x=-1 và y+1=4
=>x=-1 và y=3
c: ĐKXĐ: x<>1 và y>=2
\(\left\{{}\begin{matrix}\dfrac{1}{x-1}=a\\\sqrt{y-2}=b\left(b>=0\right)\end{matrix}\right.\)
Hệ phương trình sẽ trở thành:
a+3b=1 và 2a-3b=2
=>3a=3 và a+3b=1
=>a=1 và b=0
=>x-1=1 và y-2=0
=>x=2 và y=2
d: ĐKXĐ: x<>0 và y>=-3
Đặt \(\left\{{}\begin{matrix}\dfrac{1}{x}=a\\\sqrt{y+3}=b\left(b>=0\right)\end{matrix}\right.\)
Hệ phương trình sẽ trở thành:
4a-b=2 và a+b=3
=>5a=5 và a+b=3
=>a=1 và b=2
=>x=1 và y+3=4
=>x=1 và y=1