Hãy tìm cặp tam giác vuông đồng dạng trong Hình 8.

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Trong hình bên có 3 cặp tam giác đồng dạng là BHA và BAC; CHA và CAB; HAB và HCA.

Ta có:
AC/BC = 3/4,5 = 2/3
DE/EF = 2/3
⇒ AC/BC = DE/EF
∆ABC và ∆DFE có:
AC/BC = DE/EF = 2/3
∠BAC = ∠EDF = 90⁰
⇒ ∆ABC ∽ ∆DFE (cạnh huyền - cạnh góc vuông)
Tam giác ABC và tam giác DEF có:
\( \widehat A = \widehat D = 90^0 \)
\( \frac {AC}{DE} = \frac {BC}{EF} = \frac {3}{2} \)
\( \Rightarrow \Delta ABC \backsim \Delta DFE (ch - cgv) \)

a) ΔABC  ΔHBA vì Â = Ĥ = 90º, B̂ chung
ΔHBA vì Â = Ĥ = 90º, B̂ chung
ΔABC  ΔHAC vì Â = Ĥ = 90º, Ĉ chung
ΔHAC vì Â = Ĥ = 90º, Ĉ chung
ΔHBA  ΔHAC vì cùng đồng dạng với ΔABC.
ΔHAC vì cùng đồng dạng với ΔABC.
b) + ΔABC vuông tại A
⇒ BC2 = AB2 + AC2
(Theo định lý Pytago)


+ΔDEF vuông tại D và ΔD'E'F' vuông tại D’ có:
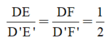
⇒ ΔDEF ∼ ΔD'E'F' (hai cạnh góc vuông)
*)Áp dụng định lí py ta go vào tam giác A’B’C’ vuông tại A’ có:
A’C’2 + A’B’2 = B’C’2
=> A’C’2 + 22 = 52
Suy ra: A’C’2 = 25 – 4 = 21 nên 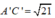
*)Áp dụng định lí py ta go vào tam giác ABC vuông tại A có:
AB2 + AC2 = BC2
Thay số: 42 + AC2 = 102
Suy ra: AC2 = 100 – 16 = 84 nên

Do đó, ∆ A’B’C’ đồng dạng với tam giác ABC ( trường hợp 2).

Để tìm 3 cặp tam giác đồng dạng với tam giác DEF, ta có thể sử dụng các định lý đồng dạng trong tam giác.
EF/DF = (DE + DF)/DF = (6+8)/8 = 7/4
ED/DF = DE/DF = 6/8 = 3/4
Vậy ta đã tìm được 3 cặp tam giác đồng dạng với tam giác DEF, đó là: DHE, EFD, EHD.

Xét cặp tam giác thứ nhất: Hình a và Hình c.
Ta có: \(\frac{3}{9} = \frac{1}{3};\frac{7}{{21}} = \frac{1}{3};\frac{{8\frac{1}{3}}}{{25}} = \frac{1}{3}\).
Do đó, tam giác ở Hình a và Hình c đồng dạng với nhau.
Xét cặp tam giác thứ hai: Hình b và Hình d.
Ta có: \(\frac{7}{{14}} = \frac{1}{2};\frac{7}{{14}} = \frac{1}{2};\frac{3}{6} = \frac{1}{2}\).
Do đó, tam giác ở Hình b và Hình d đồng dạng với nhau.

a: EP/FP=DE/DF=3/4
b: Xet ΔFHP vuông tại H và ΔFDE vuông tại D có
góc HFP chung
=>ΔFHP đồng dạng vơi ΔFDE
c: ΔFHP đồng dạng với ΔFDE
=>HP/DE=FP/FE=4/7
=>HP/9=4/7
=>HP=36/7(cm)
Xét tam giác vuông \(PQR\) có:
\(\widehat P + \widehat Q + \widehat R = 180^\circ \Leftrightarrow \widehat P + 90^\circ + 42^\circ = 180^\circ \Rightarrow \widehat P = 180^\circ - 90^\circ - 42^\circ = 48^\circ \)
Xét tam giác vuông \(UVT\) có:
\(U{V^2} = U{T^2} + V{T^2} \Leftrightarrow {6^2} = U{T^2} + {4^2} \Rightarrow U{T^2} = {6^2} - {4^2} = 20 \Rightarrow UT = 2\sqrt 5 \)
Xét tam giác vuông \(DEF\) có:
\(E{F^2} = D{E^2} + D{F^2} \Leftrightarrow E{F^2} = {9^2} + {12^2} \Rightarrow E{F^2} = 225 \Rightarrow EF = 15\)
Xét tam giác vuông \(MNK\) có:
\(K{N^2} = K{M^2} + M{N^2} \Leftrightarrow {9^2} = K{M^2} + {6^2} \Rightarrow K{M^2} = {9^2} - {6^2} = 45 \Rightarrow KM = 3\sqrt 5 \)
Xét tam giác vuông \(IGH\) có:
\(I{H^2} = H{G^2} + I{G^2} \Leftrightarrow I{H^2} = 7,{5^2} + {10^2} \Rightarrow I{H^2} = 156,25 \Rightarrow IH = 12,5\)
- Xét \(\Delta ABC\) và \(\Delta QPR\) có:
\(\widehat B = \widehat P = 48^\circ \) (chứng minh trên)
\(\widehat A = \widehat Q = 90^\circ \)
Do đó, \(\Delta ABC\backsim\Delta QPR\) (g.g)
- Xét \(\Delta UTV\) và \(\Delta KMN\) có:
\(\widehat T = \widehat M = 90^\circ \)
\(\frac{{UT}}{{KM}} = \frac{{2\sqrt 5 }}{{3\sqrt 5 }} = \frac{2}{3};\frac{{VT}}{{MN}} = \frac{4}{6} = \frac{2}{3}\)
Do đó, \(\Delta UTV\backsim\Delta KMN\) (c.g.c)
- Xét \(\Delta DEF\) và \(\Delta GHI\) có:
\(\widehat D = \widehat G = 90^\circ \)
\(\frac{{HG}}{{DE}} = \frac{{7,5}}{9} = \frac{5}{6};\frac{{IG}}{{DF}} = \frac{{10}}{{12}} = \frac{5}{6}\)
Do đó, \(\Delta DEF\backsim\Delta GHI\) (c.g.c).