Tìm tập xác định
a. y= 3/sinx - 4/cosx
b. tanx- cotx
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án là B
• Hàm số y = sin x ; y = cos x có tập xác định D = ℝ .
• Hàm số y = tan x & y = cot x có tập xác định lần lượt D = ℝ \ π 2 + k π ; D = ℝ \ k π .

a/ ĐKXĐ:
\(sin\left(\frac{\pi}{2}.sinx\right)\ne0\Rightarrow\frac{\pi}{2}.sinx\ne k\pi\)
\(\Rightarrow sinx\ne2k\)
Mà \(-1\le sinx\le1\Rightarrow sinx\ne0\Rightarrow x\ne k\pi\)
b/
\(sinx-1\ge0\Leftrightarrow sinx\ge1\Rightarrow sinx=1\)
\(\Rightarrow x=\frac{\pi}{2}+k2\pi\)
c/
\(\left\{{}\begin{matrix}sinx\ne0\\cosx\ne0\\cos2x\ne0\end{matrix}\right.\) \(\Rightarrow sin4x\ne0\)
\(\Rightarrow x\ne\frac{k\pi}{4}\)
d/
\(\left\{{}\begin{matrix}sinx\ne0\\cosx\ne0\\sinx+cotx\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}sin2x\ne0\\sin^2x+cosx\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x\ne k\pi\\-cos^2x+cosx+1\ne0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x\ne\frac{k\pi}{2}\\cosx\ne\frac{1-\sqrt{5}}{2}\\\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x\ne\frac{k\pi}{2}\\x\ne\pm arccos\left(\frac{1-\sqrt{5}}{2}\right)+k2\pi\end{matrix}\right.\)
e/
\(\left\{{}\begin{matrix}sinx\ne0\\cosx\ne1\end{matrix}\right.\) \(\Leftrightarrow sinx\ne0\Rightarrow x\ne k\pi\)

\(y=\dfrac{sinx+1}{sinx}\)
ĐKXĐ: \(sinx\ne0\Rightarrow x\ne k\pi\)
\(y=\dfrac{sin2x+cosx}{tanx-sinx}\)
ĐKXĐ: \(\left\{{}\begin{matrix}cosx\ne0\\tanx-sinx\ne0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}cosx\ne0\\sinx\left(\dfrac{1}{cosx}-1\right)\ne0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}cosx\ne0\\sinx\ne0\\cosx\ne1\end{matrix}\right.\)
\(\Rightarrow sin2x\ne0\)
\(\Rightarrow x\ne\dfrac{k\pi}{2}\)

a/ \(cosx>0\Rightarrow cosx=\sqrt{1-sin^2x}=\frac{4}{5}\)
\(\Rightarrow tanx=-\frac{3}{4}\Rightarrow A=\frac{129}{20}\)
b/ \(B=\frac{5sinx+3cosx}{3cosx-2sinx}=\frac{\frac{5sinx}{sinx}+\frac{3cosx}{sinx}}{\frac{3cosx}{sinx}-\frac{2sinx}{sinx}}=\frac{5+3cotx}{3cotx-2}=\frac{5+9}{9-2}\)
c/ \(C=\frac{sinx.cosx\left(cotx-2tanx\right)}{sinx.cosx\left(5cotx+tanx\right)}=\frac{cos^2x-2sin^2x}{5cos^2x+sin^2x}=\frac{cos^2x-2\left(1-cos^2x\right)}{5cos^2x+1-cos^2x}=\frac{3cos^2x-2}{4cos^2x+1}=...\)
d/ Không dịch được đề, ko biết mẫu số bên trái nó đến đâu cả

Hàm là vậy phải không nhỉ? \(y=\dfrac{sin^2x-3sinx}{\left(tanx-1\right)\left(cotx+1\right)}\)
ĐKXĐ: \(\left\{{}\begin{matrix}sinx\ne0\\cosx\ne0\\tanx-1\ne0\\cotx+1\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}sin2x\ne0\\tanx\ne1\\cotx\ne-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne\dfrac{k\pi}{2}\\x\ne\dfrac{\pi}{4}+k\pi\\x\ne-\dfrac{\pi}{4}+k\pi\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ne\dfrac{k\pi}{2}\\x\ne\dfrac{\pi}{4}+\dfrac{k\pi}{2}\end{matrix}\right.\)
\(\Leftrightarrow x\ne\dfrac{k\pi}{4}\)

Đáp án A
Phương pháp: Đặt sinx = a, cosx = b
Cách giải: Đặt sinx = a, cosx = b ta có a2 + b2 = 1
Khi đó 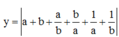
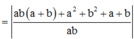
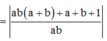
Đặt 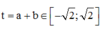
![]()
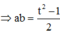
khi đó ta có : 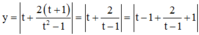
Nếu 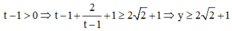
Nếu ![]()
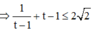
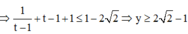
Vậy ![]()
Dấu bằng xảy ra ![]()
![]()
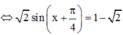
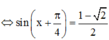

\(a,đk:\left\{{}\begin{matrix}sinx\ne0\\cosx\ne0\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x\ne k\pi\\x\ne\dfrac{\pi}{2}+k\pi\end{matrix}\right.\)
\(TXĐ:D=R/\left\{k\pi;\dfrac{\pi}{2}+k\pi\right\}\)
b, \(y=tanx-cotx=\dfrac{sinx}{cosx}-\dfrac{cosx}{sinx}\)
đk \(\left\{{}\begin{matrix}cosx\ne0\\sinx\ne0\end{matrix}\right.\)
Giống câu trên