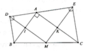
Bài 6. Cho tam giác ABC vuông tại A. Về phía ngoài tam giác ABC, vẽ hai tam giác vuông cân ADB (DA = DB) và ACE (EA = EC). Gọi M là trung điểm của BC, I là giao điểm của DM và AB, K là giao điểm của EM và AC. Chứng minh:a) Ba điểm D, A, E thẳng hàng,b) Tứ giác IAKM là hình chữ nhậtc) Tam giác DME là tam giác vuông...
Đọc tiếp
Bài 6. Cho tam giác ABC vuông tại A. Về phía ngoài tam giác ABC, vẽ hai tam giác vuông cân ADB (DA = DB) và ACE (EA = EC). Gọi M là trung điểm của BC, I là giao điểm của DM và AB, K là giao điểm của EM và AC. Chứng minh:
a) Ba điểm D, A, E thẳng hàng,
b) Tứ giác IAKM là hình chữ nhật
c) Tam giác DME là tam giác vuông cân.
a: góc DAE=góc DAB+góc BAC+góc EAC
=45+90+45=180 độ
=>D,A,E thẳng hàng
b: ΔABC vuông tại A có AM là trung tuyến
nên MA=MB=MC
MA=MB
DA=DB
=>MD là trung trực của AB
=>MD vuông góc AB tại I
MA=MC
EA=EC
=>ME là trung trực của AC
=>ME vuông góc AC tại K
Xét tứ giác AIMK có
góc AIM=góc AKM=góc KAI=90 độ
=>AIMK là hình chữ nhật