Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(\begin{array}{l}a)\frac{{4{{\rm{x}}^2} - 1}}{{16{{\rm{x}}^2} - 1}}.\left( {\frac{1}{{2{\rm{x}} + 1}} + \frac{1}{{2{\rm{x}} - 1}} + \frac{1}{{1 - 4{{\rm{x}}^2}}}} \right)\\ = \frac{{4{{\rm{x}}^2} - 1}}{{16{{\rm{x}}^2} - 1}}.\frac{{2{\rm{x}} - 1 + 2{\rm{x}} + 1 - 1}}{{\left( {2{\rm{x}} - 1} \right)\left( {2{\rm{x}} + 1} \right)}}\\ = \frac{{\left( {2{\rm{x}} - 1} \right)\left( {2{\rm{x}} + 1} \right)}}{{\left( {4{\rm{x}} - 1} \right)\left( {4{\rm{x + 1}}} \right)}}.\frac{{4{\rm{x}} - 1}}{{\left( {2{\rm{x}} - 1} \right)\left( {2{\rm{x}} + 1} \right)}}\\ = \frac{1}{{4{\rm{x}} + 1}}\\b)\left( {\frac{{x + y}}{{xy}} - \frac{2}{x}} \right).\frac{{{x^3}{y^3}}}{{{x^3} - {y^3}}}\\ = \frac{{x + y - 2y}}{{xy}}.\frac{{{x^3}{y^3}}}{{{x^3} - {y^3}}}\\ = \frac{{\left( {x - y} \right).{x^3}{y^3}}}{{xy\left( {x - y} \right)\left( {{x^2} + xy + {y^2}} \right)}} = \frac{{{x^2}{y^2}}}{{{x^2} + xy + y{}^2}}\end{array}\)
\(a)\left( { - \frac{{3{\rm{x}}}}{{5{\rm{x}}{y^2}}}} \right):\left( { - \frac{{5{y^2}}}{{12{\rm{x}}y}}} \right) = \frac{{ - 3{\rm{x}}}}{{5{\rm{x}}{y^2}}}.\frac{{ - 12{\rm{x}}y}}{{5{y^2}}} = \frac{{36{{\rm{x}}^2}y}}{{25{\rm{x}}{y^4}}}\)
b) \(\frac{4{{\text{x}}^{2}}-1}{8{{\text{x}}^{3}}-1}:\frac{4{{\text{x}}^{2}}+4\text{x}+1}{4{{\text{x}}^{2}}+2\text{x}+1}=\frac{4{{\text{x}}^{2}}-1}{8{{\text{x}}^{3}}-1}.\frac{4{{\text{x}}^{2}}+2\text{x}+1}{4{{\text{x}}^{2}}+4\text{x}+1}\)
\(=\frac{\left( 2\text{x}-1 \right)\left( 2\text{x}+1 \right)\left( 4{{\text{x}}^{2}}+2\text{x}+1 \right)}{\left( 2\text{x}-1 \right)\left( 4{{\text{x}}^{2}}+2\text{x}+1 \right){{\left( 2\text{x}+1 \right)}^{2}}}=\frac{1}{2\text{x}+1}\).
Khẳng định C là khẳng định sai vì:
Nếu: \(\frac{{x + 1}}{{x - 1}} = \frac{{{x^2} + x + 1}}{{{x^2} - x + 1}}\)
\(\begin{array}{l} \Rightarrow \frac{{x + 1}}{{x - 1}} - \frac{{{x^2} + x + 1}}{{{x^2} - x + 1}} = 0\\ \Rightarrow \frac{{\left( {x + 1} \right)\left( {{x^2} - x + 1} \right) - \left( {{x^2} + x + 1} \right)\left( {x - 1} \right)}}{{\left( {x - 1} \right)\left( {{x^2} - x + 1} \right)}} = 0\\ \Rightarrow \frac{{\left( {{x^3} + 1} \right) - \left( {{x^3} - 1} \right)}}{{\left( {x - 1} \right)\left( {{x^2} - x + 1} \right)}} = \frac{2}{{\left( {x - 1} \right)\left( {{x^2} - x + 1} \right)}} = 0\end{array}\)
\( \Rightarrow \) vô lý
Cặp phân thức có cùng mẫu thức: \(\frac{{5{\rm{x}} + 10}}{{4{\rm{x}} - 8}}\) và \(\frac{{4 - 2{\rm{x}}}}{{4\left( {x - 2} \right)}}\)
\(a)\frac{{{x^2} - 3{\rm{x}} + 1}}{{2{{\rm{x}}^2}}} + \frac{{5{\rm{x}} - 1 - {x^2}}}{{2{{\rm{x}}^2}}} = \frac{{{x^2} - 3{\rm{x}} + 1 + 5{\rm{x}} - 1 - {x^2}}}{{2{{\rm{x}}^2}}} = \frac{{2{\rm{x}}}}{{2{{\rm{x}}^2}}}\)
\(b)\frac{y}{{x - y}} + \frac{x}{{x + y}} = \frac{{y\left( {x + y} \right) + x\left( {x - y} \right)}}{{\left( {x - y} \right)\left( {x + y} \right)}} = \frac{{xy + {y^2} + {x^2} - xy}}{{{x^2} - {y^2}}} = \frac{{{x^2} + {y^2}}}{{{x^2} - {y^2}}}\)
\(c)\frac{x}{{2{\rm{x}} - 6}} + \frac{9}{{2{\rm{x}}\left( {3 - x} \right)}} = \frac{x}{{2\left( {x - 3} \right)}} - \frac{9}{{2{\rm{x}}\left( {x - 3} \right)}} = \frac{{{x^2}}}{{2{\rm{x}}\left( {x - 3} \right)}} - \frac{9}{{2{\rm{x}}\left( {x - 3} \right)}} = \frac{{{x^2} - 9}}{{2{\rm{x}}\left( {x - 3} \right)}} = \frac{{\left( {x - 3} \right)\left( {x + 3} \right)}}{{2{\rm{x}}\left( {x - 3} \right)}} = \frac{{x + 3}}{{2{\rm{x}}}}\)
a) Tìm thương và dư (nếu có) trong các phép chia \(\left( {3{{\rm{x}}^4}y - 9{{\rm{x}}^3}{y^2} - 21{{\rm{x}}^2}{y^2}} \right):\left( {3{{\rm{x}}^2}y} \right)\)
• Sử dụng lệnh Division(<đa thức bị chia>, <đa thức chia>) để tìm thương và dư của phép chia hai đa thức.
• Nhập biểu thức trên dòng lệnh của cửa sổ CAS sau đó nhấn Enter, kết quả sẽ được hiển thị ngay bên dưới.
Vậy phép chia hai đa thức \(\left( {3{{\rm{x}}^4}y - 9{{\rm{x}}^3}{y^2} - 21{{\rm{x}}^2}{y^2}} \right)\) cho \(3{{\rm{x}}^2}y\), ta được thương là \({x^2} - 3{\rm{x}}y - 7y\) và dư 0.
b) Tìm thương và dư (nếu có) trong các phép chia (2x3 + 5x2 – 2x + 12) : (2x2 – x + 1).
• Sử dụng lệnh Division(<đa thức bị chia>, <đa thức chia>) để tìm thương và dư của phép chia hai đa thức.
• Nhập biểu thức trên dòng lệnh của cửa sổ CAS sau đó nhấn Enter, kết quả sẽ được hiển thị ngay bên dưới.
Vậy phép chia hai đa thức (2x3 + 5x2 – 2x + 12) cho (2x2 – x + 1), ta được thương là x + 3 và dư 9.
Nhập biểu thức trên dòng lệnh của cửa sổ CAS sau đó nhấn Enter, kết quả sẽ được hiển thị ngay bên dưới.
\(a)\frac{{5{\rm{x}} + 10}}{{25{{\rm{x}}^2} + 50}} = \frac{{5\left( {x + 2} \right)}}{{25\left( {{x^2} + 2} \right)}} = \frac{{x + 2}}{{5\left( {{x^2} + 2} \right)}}\)
\(b)\frac{{45{\rm{x}}\left( {3 - x} \right)}}{{15{\rm{x}}{{\left( {x - 3} \right)}^2}}} = \frac{{3\left( {3 - x} \right)}}{{{{\left( {x - 3} \right)}^2}}}\)
\(c)\frac{{{{\left( {{x^2} - 1} \right)}^2}}}{{\left( {x + 1} \right)\left( {{x^3} + 1} \right)}} = \frac{{\left( {{x^2} - 1} \right)\left( {{x^2} - 1} \right)}}{{\left( {x + 1} \right)\left( {x + 1} \right)\left( {{x^2} - x + 1} \right)}} = \frac{{\left( {x + 1} \right)\left( {x - 1} \right)\left( {x + 1} \right)\left( {x - 1} \right)}}{{\left( {x + 1} \right)\left( {x + 1} \right)\left( {{x^2} - x + 1} \right)}} = \frac{{{{\left( {x - 1} \right)}^2}}}{{{x^2} - x + 1}}\)
a) Ta có: \(P = \frac{{x + 1}}{{{x^2} - 1}} = \frac{{x + 1}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} = \frac{1}{{x - 1}}\)
Suy ra: \(Q = \frac{1}{{x - 1}}\)
b) Thay x = 11 vào P ta được: \(P = \frac{{11 + 1}}{{{{11}^2} - 1}} = \frac{1}{{10}}\)
Thay x = 11 vào Q ta được: \(Q = \frac{1}{{11 - 1}} = \frac{1}{{10}}\)
Hai kết quả P = Q tại x = 11
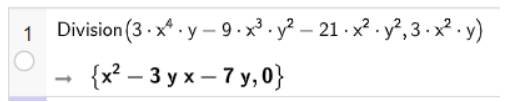
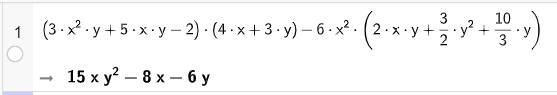
\(\begin{array}{l}a)\frac{{4{\rm{x}} - 6}}{{5{{\rm{x}}^2} - x}}.\frac{{25{{\rm{x}}^2} - 10{\rm{x}} + 1}}{{27 + 8{{\rm{x}}^3}}}\\ = \frac{{ - 2\left( {3 - 2{\rm{x}}} \right)}}{{x\left( {5{\rm{x}} - 1} \right)}}.\frac{{{{\left( {5{\rm{x}} - 1} \right)}^2}}}{{\left( {3 - 2{\rm{x}}} \right)\left( {9 + 6{\rm{x}} + 4{{\rm{x}}^2}} \right)}}\\ = \frac{{ - 2\left( {5{\rm{x}} - 1} \right)}}{{x\left( {9 + 6{\rm{x}} + 4{{\rm{x}}^2}} \right)}}\\b)\frac{{2{\rm{x}} + 10}}{{{{\left( {x - 3} \right)}^2}}}:\frac{{{{\left( {x + 5} \right)}^3}}}{{{x^2} - 9}}\\ = \frac{{2{\rm{x}} + 10}}{{{{\left( {x - 3} \right)}^2}}}.\frac{{{x^2} - 9}}{{{{\left( {x + 5} \right)}^2}}}\\ = \frac{{2\left( {x + 5} \right)\left( {x - 3} \right)\left( {x + 3} \right)}}{{{{\left( {x - 3} \right)}^2}{{\left( {x + 5} \right)}^3}}}\\ = \frac{{2\left( {x + 3} \right)}}{{\left( {x - 3} \right){{\left( {x + 5} \right)}^2}}}\end{array}\)