Question

[The gift]

Cho tam giác ABC, vuông tại A đường cao AH. Biết AH = 2 căn 3, góc BAH = 60 độ. Tính bán kính đường tròn đi qua ba đỉnh của tam giác ABC

Answer 1

[Nguyễn Đức Trí]

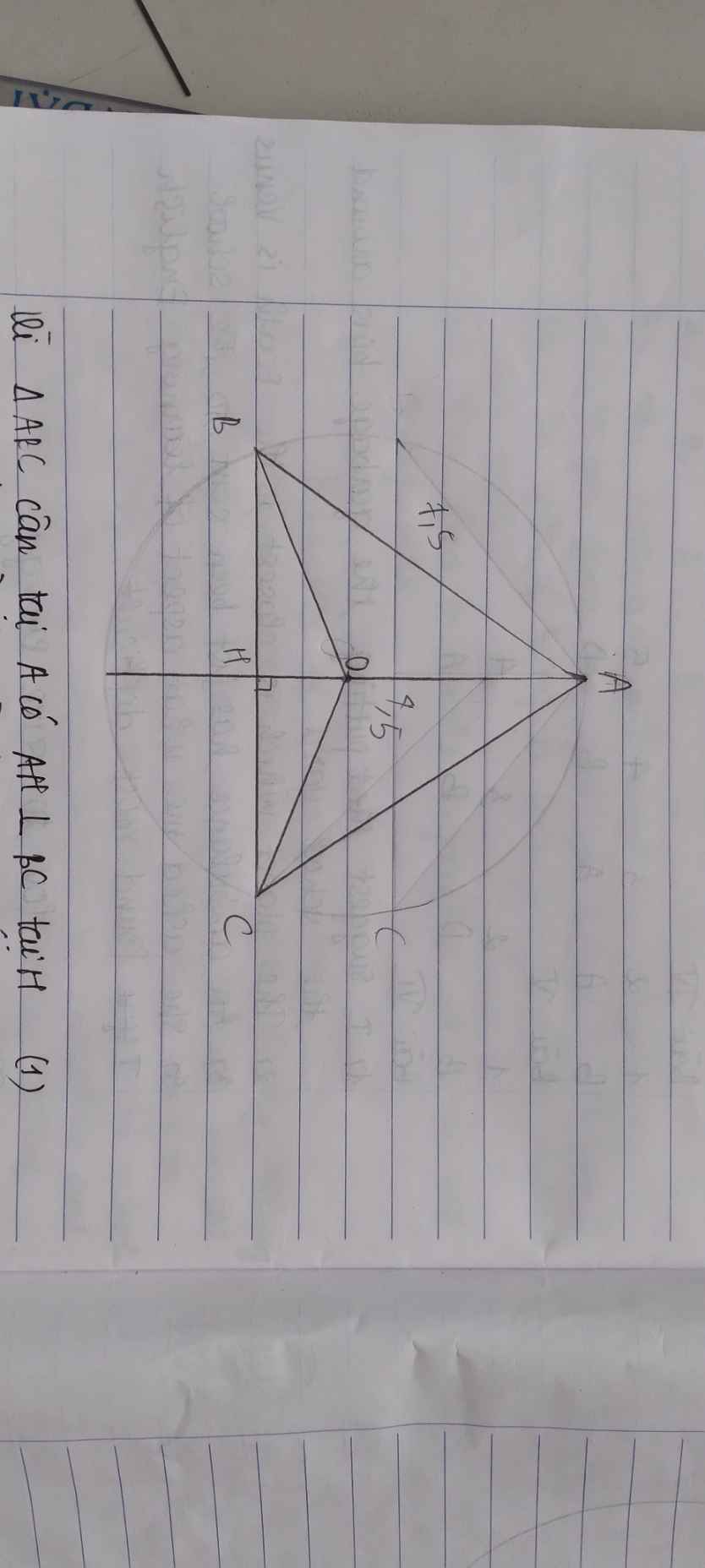
Xét \(\Delta\) vuông tại H \(ABH\) có :

\(tan\widehat{BAH}=tan60^o=\dfrac{BH}{AH}\Rightarrow BH=AH.tan60^o=2\sqrt[]{3}.\sqrt[]{3}=6\)

Xét \(\Delta\) vuông tại H \(ACH\) có :

\(\widehat{HAC}=90^o-\widehat{BAH}=90^o-60^o=30^o\)

\(tan\widehat{HAC}=tan30^o=\dfrac{CH}{AH}\Rightarrow CH=AH.tan30^o=2\sqrt[]{3}.\dfrac{1}{\sqrt[]{3}}=2\)

Tâm đường tròn ngoại tiếp tam giác vuông ABC là trung điểm BC

\(\Rightarrow\) Bán kính đường tròn này là :

\(R=\dfrac{BC}{2}=\dfrac{BH+CH}{2}=\dfrac{6+2}{2}=4\)