Cho tam giác \(ABC\) có \(BC=15\) \(cm\), \(AC=20\) \(cm\), \(AB=25\) \(cm\).\(a\). Tính độ dài đường cao \(CH\) của tam giác \(ABC\).\(b\). Gọi \(CD\) là đường phân giác của tam giác \(ACH\). Chứng minh tam giác \(BCD\) cân.\(c\). Chứng...
Đọc tiếp
Cho tam giác \(ABC\) có \(BC=15\) \(cm\), \(AC=20\) \(cm\), \(AB=25\) \(cm\).
\(a\). Tính độ dài đường cao \(CH\) của tam giác \(ABC\).
\(b\). Gọi \(CD\) là đường phân giác của tam giác \(ACH\). Chứng minh tam giác \(BCD\) cân.
\(c\). Chứng minh: \(BC^2+CD^2+BD^2=3CH^2+2BH^2+DH^2\)
(tính chất đường phân giác)
(tính chất tỉ lệ thức)
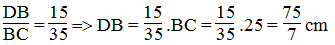
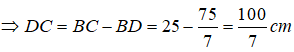
a: Xét ΔCAB có CA^2+CB^2=AB^2
nên ΔCAB vuông tại C
Xét ΔCAB vuông tại C có CH là đường cao
nên CH*AB=CA*CB
=>CH*25=15*20=300
=>CH=12(cm)
b: góc BCD+góc ACD=90 độ
góc BDC+góc HCD=90 độ
mà góc ACD=góc HCD
nên góc BCD=góc BDC
=>ΔBDC cân tại B
c: BC^2+BD^2+CD^2
=BC^2+BC^2+CD^2
=2BC^2+CD^2
=2(BH^2+HC^2)+CH^2+HD^2
=2BH^2+3CH^2+DH^2