Hình bình hành có độ dài một cạnh là 4, độ dài hai đường chéo là 6 và 8. Tính độ dài cạnh kề với cạnh có độ dài bằng 4.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 10 2021
TL:
a) Diện tích hình vuông là:
5 x 5 = 25 ( cm2 )
Đ/S: 25cm2
PT
1
27 tháng 3 2021
Gọi O là giao của hai đường chéo
Ta có: \(\overrightarrow{AB}=\overrightarrow{AO}+\overrightarrow{OB}\); \(\overrightarrow{AD}=\overrightarrow{AO}+\overrightarrow{OD}=\overrightarrow{AO}-\overrightarrow{OB}\)
Suy ra : \(\overrightarrow{AB}.\overrightarrow{AD}=AO^2-OB^2=3^2-4^2=-7\)
\(\Leftrightarrow AB^2.AD^2=49\)\(\Leftrightarrow AD^2=\dfrac{49}{16}\Leftrightarrow AD=\dfrac{7}{4}\)
HQ
Hà Quang Minh
Giáo viên
10 tháng 10 2023
a) \(a = 20cm;h = 5cm\).
Áp dụng công thức tính diện tích ta có:
\(S =20.5=100 \left( {c{m^2}} \right)\).
b) \(m = 5\left( m \right);n = 20\left( {dm} \right) = 2\left( m \right)\)
\( \Rightarrow S = \frac{{m.n}}{2} = \frac{{5.2}}{2} = 5\left( {{m^2}} \right)\)
c) \(a = 5\left( m \right);b = 3,2\left( m \right);h = 4\left( m \right)\)
\( \Rightarrow S = \frac{{\left( {a + b} \right).h}}{2} = \frac{{\left( {5 + 3,2} \right).4}}{2} = 16,4\left( {{m^2}} \right)\).
CM
10 tháng 3 2017
Gọi x (cm) là độ dài đường cao thứ hai ứng với cạnh 8cm của hình bình hành (0 < x < 5)
Theo công thức tính diện tích hình bình hành ta có phương trình:
6.5 = 8.x ⇔ 8x =30 ⇔ x = 3,75 (tmđk)
Vậy độ dài đường cao thứ hai là 3,75cm
HQ
Hà Quang Minh
Giáo viên
21 tháng 7 2023
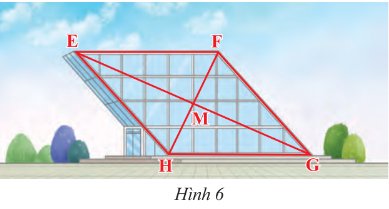
Do tứ giác EFGH là hình bình hành \(\Rightarrow\left\{{}\begin{matrix}HG=EF=40m\\HF=2HM=2\cdot16=32m\\EG=2EM=2\cdot36=72m\end{matrix}\right.\)
KL
hình bình hành có chu vi là 146m, hiệu độ dài hai cạnh liền kề là 15m. Tính độ dài hai cạnh liền kề.
5
28 tháng 5 2022
Độ dài cạnh thứ nhất là:
(73+15):2=44(m)
Độ dài cạnh thứ hai là 44-15=29(m)
Để tính độ dài cạnh kề với cạnh có độ dài bằng 4, ta có thể sử dụng định lý Pythagoras. Định lý này cho biết rằng trong một tam giác vuông, bình phương của độ dài cạnh huyền (đường chéo dài nhất) bằng tổng bình phương của độ dài hai cạnh góc vuông.
Trong trường hợp này, ta có độ dài hai đường chéo là 6 và 8. Để tìm độ dài cạnh kề với cạnh có độ dài bằng 4, ta cần tìm độ dài cạnh còn lại của hình bình hành.
Áp dụng định lý Pythagoras, ta có: (độ dài cạnh kề)^2 + (độ dài cạnh kề)^2 = (độ dài đường chéo)^2
Đặt độ dài cạnh kề là x, ta có: x^2 + 4^2 = 6^2
Giải phương trình trên, ta có: x^2 + 16 = 36 x^2 = 36 - 16 x^2 = 20 x = √20
Vậy độ dài cạnh kề với cạnh có độ dài bằng 4 là √20.